在复杂度分析中.算法通过子程序来获得所求问题的局部信息。不同的算法需要获得不同的局部信息。比如,对于梯度法来说,对任意给定输入 , 子程序
返回函数值信息
和梯度信息
; 对于次梯度法, 则需要返回次梯度信息
; 对于牛顿法, 需要返回二阶导数信息
.
这些子程序(Oracle)都是事先给定的, 复杂度分析理论并不衡量这些子程序的求解复杂度. 我们假设这些子程序 具有局部性和黑盒性.
- 子程序
是唯一局部信息来源: 数值算法唯一可获得的有关目标优化问题的局部信息来源于子程序.
- 子程序
具有局部稳定性: 调用子程序时, 对测试点
做微小的扰动, 返回的局部信息
变化不大.
其中第二条是对算法进行收敛性分析的关键假设. 例如, 在分析梯度法的收敛性时, 由于 或
, 我们需要假设存在某一常数
使得
也就是假设目标函数具有Lipschtiz连续性.或者目标函数的导数具有Lipschtiz连续性(甚至是在牛顿法中还要求目标函数的二阶导数Lipschtiz连续)。对于没有这样性质的优化问题的目标函数,数值算法有可能很难收敛, 或者收敛性质很差. 其实这也解释了前面的文章中多次出现了Lipschtiz连续性这一假设的作用.
子程序的类别:
(zero order oracle): 适用于无导数优化算法, 对于任意给定的
返回
.
(first order oracle): 适用于梯度法, 返回函数在
处的函数值和一阶导数信息,
或
(second order oracle): 适用于牛顿法, 返回函数在
处的函数值和一, 二阶导数信息,
(stochostic first order oracle): 适用于随机梯度法, 返回
在
的函数值和一阶随机梯度信息
.
(projection/prox-operator oracle): 适用于投影梯度法, 返回
在
上的投影
对于求解合成函数 的临近点梯度法, 返回
的邻近点投影
(linear optimization oracle): 适用于条件梯度法, 当
是多面体时, 对给定
返回线性规划的解
.
(separation oracle): 适用于椭球法, 对于有界闭约束集合
, 给定点
, 如果
则返回真, 否则返回一个向量
在
处形成一个分割超平面:
.
上述子程序的任意组合可以形成不同算法所需要的子程序. 比如 组成椭球法和重心法每一步所需要调用的子程序;
组成投影梯度法所需的子程序;
分别组成条件梯度法, 随机梯度法, 随机条件梯度法所需要调用的子程序.
我们定义两种测度来衡量算法 在问题
上的计算复杂度:
- 分析复杂度(Analytical complexity): 将问题
求解到精度
总共所需要调用子程序
的次数。
- 算术复杂度(Arithmetical complexity): 将问题
求解到精度
总共所需要执行的算术操作(包括子程序
内部的操作和算法本身的橾作)。
算术复杂度更能实际体现算法的效率。但当我们用特定算法 求解某一具体问题
时候,如果可以知道子程序
的复杂度. 我们可以很容易地从分析复杂度推出算术复杂度。因此在本文中. 我们主要研究算法
在问题集合
上的分析复杂度。
分析复杂度与优化收敛性分析理论中的收敛率有一定的关系。
- 次线性收敛率(Sublinear rate):
, 其中
为常数, 令
得到
, 对应的分析复杂度为
.
- 线性收敛率(Linear rate):
其中
为常数, 令
得到
, 对应的分析复杂度为
.
- 二阶收敛率(Quadratic rate):
, 对应的分析复杂度为
.
假设序列 收敛到一个数
(这里的
不是Lipschtiz常数, 注意区分), 定义Q-收敛率:
即收敛率是指连续两次误差比值的极限, 为保证极限收敛需满足 .
- 如果在
时,
, 我们称当前的收敛为Q-超线性收敛(converge Q-superlinearly)
, 我们称当前的收敛为Q-次线性收敛(converge Q-sublinearly)
- 如果
, 那么我们称该序列对数(logarithmically)收敛于
. 注意和前面的两个不同, 对数收敛不称为Q-对数.
为进一步对收敛进行分类, 定义收敛的阶(order)如下.
对于 , 我们称序列是
阶收敛到
的, 当且仅当
对于常数 (该常数不需要小于1)成立. 在实践中, 可以做出以下的划分:
被称为线性收敛
被称为2次(quadratic)收敛
被称为3次(cubic)收敛
- 以此类推
在上面的定义中 表示商(quotient), 因为这些项都是使用两个相邻项之间的商来定义的, 一般情况下都可以省略.
怎么知道是几阶的?
实践中通常通过求解下面的问题来估算收敛的阶次 :
Q-收敛的定义有一个缺点, 即它不能涵盖某些序列, 例如我们接下来要说的 序列, 其收敛速度很快, 但是同时速度也是在变化的. 因此下面给出一种拓展的R-收敛的定义:
假设 收敛到
, 如果存在一个序列
使得:
且 收敛Q线性到0, 那么我们称该序列是R-线性收敛到
.
的前缀表示的是root
例子:
第一个例子
考虑序列: , 可以看到随着
的增加这个序列会收敛到
.
那么上面序列的收敛类型是什么呢?
为了搞清楚我们把该序列嵌入到Q-线性收敛的定义中:
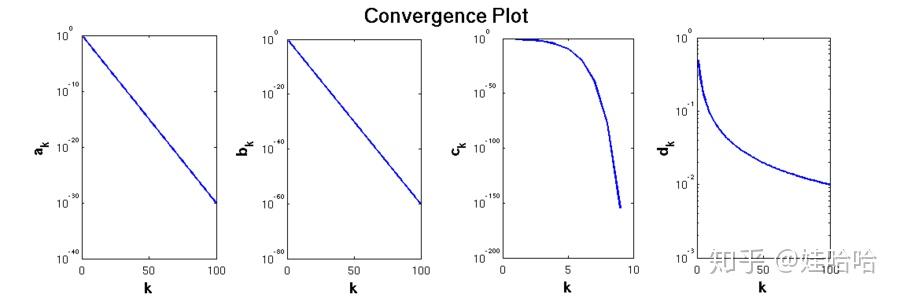
因此我们可以看出该序列Q-线性收敛, 且收敛速率为 .
更一般地来说, 对于任意的 , 序列
以速率
线性收敛.
第二个例子:
在R收敛的定义下, 同样以速率1/2收敛到0, 但是在Q收敛下不成立.
第三个例子:
是超线性收敛的. 实际上它是二次收敛的.
第四个例子
是次线性且对数收敛的.
以上四个例子的收敛曲线如下图所示
下面给出几个复杂度分析的例子.
例1.1(盒约束全局优化问题的复杂度上界和下界)
考虑如下全局最优化的问题:
其中约束集合 是一个
维的盒子
, 其中
表示
的第
个元素的值. 在
中我们使用
范数来做为距离的度量. 假设函数
在
上相对于
范数是Lipschitz连续的:
问题模型: 盒约束全局优化问题模型 的三个部分:
- 全局信息
:
在
上
-Lipschtiz连续 ,
- 局部信息
:
子程序, 对于任意给定的
返回函数值
,
- 解的精度
: 求近似解
, 使得
.
对于问题集合1.1 中的任何一个具体优化问题
, 我们考虑求解它的一个简单解算法
:

无导数全局优化算法 将
均匀分成
个网格点, 然后计算每个网格点上的函数值, 最后返回函数值最小的网格点作为上面问题的近似解. 容易看到,
也属于我们的抽象迭代算法框架, 它需要迭代
次, 全部遍历测试点列才能找到函数值最小的点. 只是它是按照顺序更新新的点, 并未对收集的历史点列信息做任何实际操作. 于是我们可以衡量算法
的效率.
定理1.2 记 为上面问题模型(1)的全局最优解, 利用无导数全局优化算法1.2求解(1)有,
对于问题模型(1)中的每一个具体的问题 , 算法
的分析复杂度满足:
.
其中 表示取
的整数部分.
证明:
由算法1.2不难看出问题模型(1)的全局最优解 要么落在测试点列上, 要么被测试点列组成的网格包含. 即存在
使得
这里 当且仅当
对任意
成立. 注意到
对任意
成立, 且
记 , 构造点
如下:
可以看到 . 因此
注意到 也属于测试点列, 因此
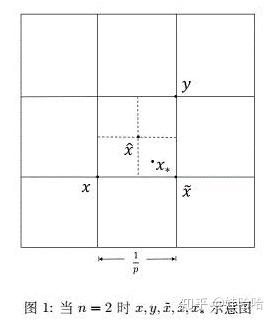
当 时,
的关系如图1. 取
, 则
. 由定理1.2我们有
注意到我们需要调用 次的函数值, 因此算法
的分析复杂度满足不等式(2). 那么它的收敛率怎么算呢?
可以看出算法 的收敛速度与盒约束集合每一维划分的密度
有关. 复杂度分析中, 我们更关心算法的分析复杂度, 也就是
在得到
精度的近似解时, 需要调用用少次
子程序. 于是我们有了如下关于
复杂度上界的推论.
在不等式(2)两边关于问题集合 中取极大, 我们可以得到问题集合
的复杂度上界的估值:
也就是说, 存在一个算法(比如 )在解决
中每个具体问题
时(近似解满足
). 所需要调用的
子程序次数之多不超过
关于结论(3), 我们会提出一些问题.
- 我们在估计算法
时太过粗略, 是否存在比式(3)更好的界?
- 是否存在其他算法, 其效率比
要好?
要回答这两个问题, 我们就需要推导问题集合 的复杂度下界.
我们首先需要定义问题集合 的解算法集合
.
定理1.3 令 , 对于式(1)对应的问题集合
来说, 对于其中每一个具体问题
, 对于其解算法集合
中任意一个算法
, 其分析复杂度满足
.
证明:
考虑 子程序定义的解算法集合
中的任意一个解算法
.
通过对约束集合
进行采样得到测试点列
. 然后在每一个测试点列上调用
子程序, 通过处理(排序)子程序返回的信息(函数值信息)得到最优近似解.
中解算法之间的差异仅在于测试点列的选取方式, 比如算法1.2是在
上采用均匀采样的方式.
我们现在利用反证法来证明定理1.3.
令采样的测试点列个数 , 若存在
中的一个解算法
.
在求解问题模型(1) 得到 精度时调用
子程序的次数
(这个是我们要推倒的悖论).
我们只需要证明存在某一目标函数,使得 在求解该目标函数时, 迭代
次后的精度大于等于
即可证伪.
由于在
上采样的测试点列个数
, 采样点的个数少于集合中总的点的个数.
因此存在非测试点 (并非所有点都参与了测试)以及集合
使得
中不包含任何测试点。
令 , 在集合不包含任何测试点的集合
上构造函数:
令 当
是测试点时,
(这里表示的是差集, 即相当于
).
注意到 , 因此
, 其图像如图2所示:
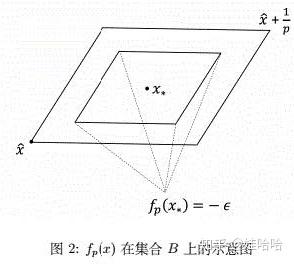
注意到 是
-Lipschtiz连续的:
.
全局最优解为 .
利用 求解
时,由于在所要测试点列处谓用
子程序都返回
, 因此求得近似最优解为
, 于是有
因此我们得到结论若测试点列的个数 ( 子程序
的调用次数)则对应的解算法求得的精度不可能比
更好。即问题模型(1)的复杂度下界为
.




