其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》,清华大学出版社,雷明著,由SIGAI公众号作者倾力打造。
本文PDF全文链接:理解贝叶斯优化
贝叶斯优化是一种黑盒优化算法,用于求解表达式未知的函数的极值问题。算法根据一组采样点处的函数值预测出任意点处函数值的概率分布,这通过高斯过程回归而实现。根据高斯过程回归的结果构造采集函数,用于衡量每一个点值得探索的程度,求解采集函数的极值从而确定下一个采样点。最后返回这组采样点的极值作为函数的极值。这种算法在机器学习种被用于AutoML算法,自动确定机器学习算法的超参数。某些NAS算法也使用了贝叶斯优化算法。
本文系统地介绍贝叶斯优化的原理,首先介绍黑盒优化问题,给出贝叶斯优化算法的全貌。然后介绍高斯过程回归的原理,它是贝叶斯优化算法的两个核心模块之一。最后介绍贝叶斯优化的详细过程,核心是采集函数的构造。本文是对《机器学习-原理、算法与应用》一书的补充,限于篇幅,在这本书中没有讲述高斯过程回归和自动化机器学习的知识。
绝大多数机器学习算法都有超参数。这些超参数可以分为两种类型,定义模型及结构本身的参数,目标函数与优化算法(求解器)所需的参数。前者用于训练和预测阶段,后者只用于训练阶段。在训练时需要人工设定它们的值,通过反复试验获得好的结果,整个过程会耗费大量的时间和人力成本。因此如何自动确定超参数的值是AutoML中一个重要的问题。问题的核心是自动搜索出最优超参数值以最大化预期目标。因此可抽象为函数极值问题,优化变量为超参数,函数值为机器学习模型的性能指标如准确率、预测速度。
黑盒优化问题目标函数的表达式未知,只能根据离散的自变量取值得到对应的目标函数值。超参数优化属于黑盒优化问题,在优化过程中只能得到函数的输入和输出,不能获取优化目标函数的表达式和梯度信息,这一特点给超参数优化带来了困难。对于某些机器学习模型,超参数数量较大,是高维优化问题。对模型进行评估即计算目标函数的值在很多情况下成本高昂,因为这意味着要以某种超参数配置训练机器学习模型,并在验证集上计算精度等指标。常用的超参数优化方法有网格搜索(Grid search),随机搜索(Random search),遗传算法,贝叶斯优化(Bayesian Optimization)等,接下来分别进行介绍。
网格搜索是最简单的做法,它搜索一组离散的取值情况,得到最优参数值。对于连续型的超参数,对其可行域进行网格划分,选取一些典型值进行计算。假设需要确定的超参数有2个,第1个的取值为[0,1]之间的实数,第2个的取值为[1,2]之间的实数。则可以按照如下的方案得到若干离散的取值,以这些值运行算法:
将第1个参数均匀的取3个典型值,将第2个参数均匀的取3个典型值。对于所有的取值组合运行算法,将性能最优的取值作为超参数的最终取值。这种方法如图1所示。
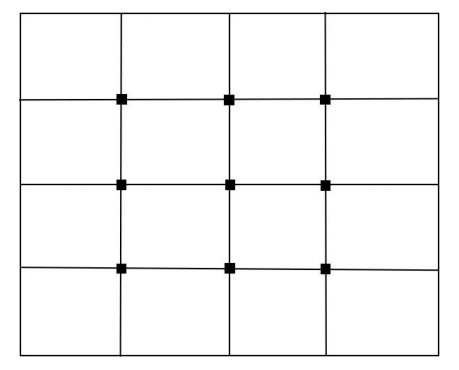
网格搜索随着参数数量的增加呈指数级增长,因此对于超参数较多的情况,该方法面临性能上的问题。著名的支持向量机开源库libsvm使用了网格搜索算法确定SVM的超参数。
随机搜索做法是将超参数随机地取某些值,比较各种取值时算法的性能,得到最优超参数值,其原理如图2所示。
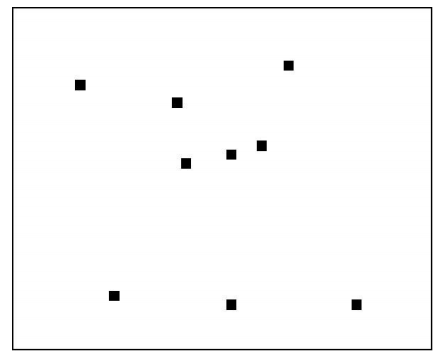
对于如何生成随机取值,有多种不同的策略。通常的做法是用均匀分布的随机数进行搜索,也可以使用更复杂的启发式搜索策略。
网格搜索和随机搜索没有利用已搜索点的信息,使用这些信息指导搜索过程可以提高结果的质量以及搜索的速度。贝叶斯优化(Bayesian optimization algorithm,简称BOA)利用之前已搜索点的信息确定下一个搜索点,用于求解维数不高的黑盒优化问题。
算法的思路是首先生成一个初始候选解集合,然后根据这些点寻找下一个有可能是极值的点,将该点加入集合中,重复这一步骤,直至迭代终止。最后从这些点中找出极值点作为问题的解。
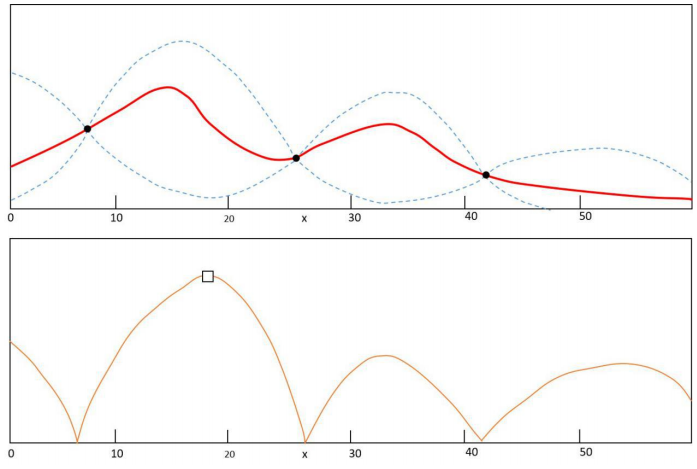
这里的关键问题是如何根据已经搜索的点确定下一个搜索点。贝叶斯优化根据已经搜索的点的函数值估计真实目标函数值的均值和方差(即波动范围),如图3所示。上图中红色的曲线为估计出的目标函数值即在每一点出处的目标函数值的均值。现在有3个已经搜索的点,用黑色实心点表示。两条虚线所夹区域为在每一点处函数值的变动范围,在以均值即红色曲线为中心,与标准差成正比的区间内波动。在搜索点处,红色曲线经过搜索点,且方差最小,在远离搜索点处方差更大,这也符合我们的直观认识,远离采样点处的函数值估计的更不可靠。
根据均值和方差可以构造出采集函数(acquisition function),即对每一点是函数极值点的可能性的估计,反映了每一个点值得搜索的程度,该函数的极值点是下一个搜索点,如图3的下图所示。下图中的矩形框所表示的点是采集函数的极大值点,也是下一个搜索点。
算法的核心由两部分构成:对目标函数进行建模即计算每一点处的函数值的均值和方差,通常用高斯过程回归实现;构造采集函数,用于决定本次迭代时在哪个点处进行采样。
多维高斯分布具有诸多优良的性质。高斯过程(Gaussian Process,GP)用于对一组随着时间增长的随机向量进行建模,在任意时刻随机向量的所有子向量均服从高斯分布。假设有连续型随机变量序列
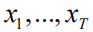
,如果该序列中任意数量的随机变量构成的向量
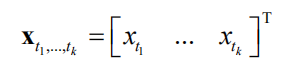
均服从多维正态分布,则称此随机变量序列为高斯过程。特别地,假设当前有k
个随机变量
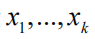
,它们服从k维正态分布
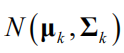
。其中均值向量
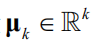
,协方差矩阵
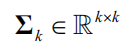
。加入一个新的随机变量
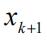
之后,随机向量
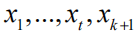
服从k+1维正态分布
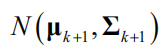
。其中均值向量
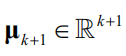
,协方差矩阵
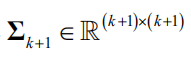
。由于正态分布的积分能得到解析解,因此可以方便地得到边缘概率与条件概率。均值向量与协方差矩阵的计算将在稍后讲述。
在机器学习中,算法通常情况下是根据输入值x预测出一个最佳输出值y,用于分类或回归任务。这种情况将y看作普通的变量。某些情况下我们需要的不是预测出一个函数值,而是给出这个函数值的后验概率分布
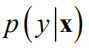
。此时将函数值看作随机变量。对于实际应用问题,一般是给定一组样本点
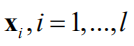
,根据它们拟合出一个假设函数,给定输入值x,预测其标签值y或者其后验概率
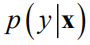
。高斯过程回归对应的是第二种方法。
高斯过程回归(Gaussian Process Regression,GPR)对表达式未知的函数(黑盒函数)的一组函数值进行贝叶斯建模,给出函数值的概率分布。假设有黑盒函数f(x)
实现如下映射
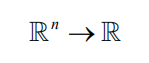
高斯过程回归可以根据某些点
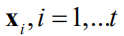
以及在这些点处的函数值
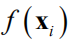
得到一个模型,拟合此黑盒函数。对于任意给定的输入值x可以预测出f(x),并给出预测结果的置信度。事实上模型给出的是f(x)的概率分布。
高斯过程回归假设黑盒函数在各个点处的函数值f(x)都是随机变量,它们构成的随机向量服从多维正态分布。对于函数f(x),x有若干个采样点
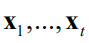
,在这些点处的函数值构成向量
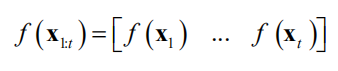
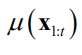
是
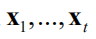
的简写,后面沿用此写法。高斯过程回归假设此向量服从k维正态分布
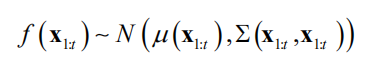
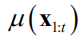
是高斯分布的均值向量
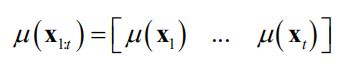
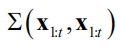
是协方差矩阵
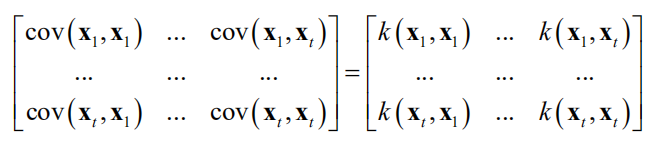
问题的核心是如何根据样本值计算出正态分布的均值向量和协方差矩阵。均值向量通过使用均值函数μ(x)根据每个采样点x计算而构造。协方差通过核函数
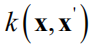
根据样本点对
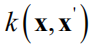
计算得到,也称为协方差函数。核函数需要满足下面的要求。
1. 距离相近的样本点 和
之间有更大的正协方差值,因为相近的两个点的函数值也相似,有更强的相关性;
2. 保证协方差矩阵是对称半正定矩阵。根据任意一组样本点计算出的协方差矩阵都必须是对称半正定矩阵。
通常使用的是高斯核与Matern核。高斯核定义为
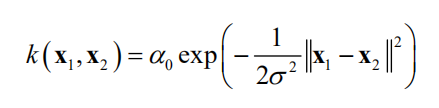
,
为核函数的参数。显然该核函数满足上面的要求。高斯核在支持向量机等其他机器学习算法中也有应用。
Matern核定义为
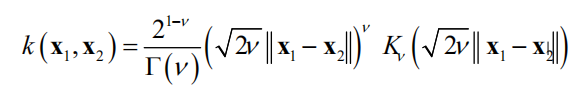
其中
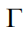
是伽马函数, 是贝塞尔函数(Bessel function),
是人工设定的正参数。用核函数计算任意两点之间的核函数值,得到核函数矩阵
作为协方差矩阵的估计值。
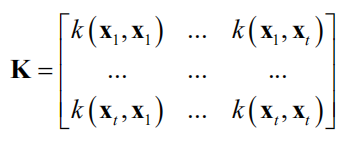
接下来介绍均值函数的实现。可以使用下面的常数函数
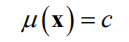
最简单的可以将均值统一设置为0
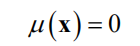
即使将均值统一设置为常数,因为有方差的作用,依然能够对数据进行有效建模。如果知道目标函数 的结构,也可以使用更复杂的函数。
在计算出均值向量与协方差矩阵之后,可以根据此多维正态分布来预测 在任意点处函数值的概率分布。假设已经得到了一组样本值
以及其对应的函数值
,接下来要预测新的点
的函数值
的数学期望和方差
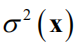
。如果令
加入该点之后
服从 维正态正态分布。将均值向和协方差矩阵进行分块,可以写成
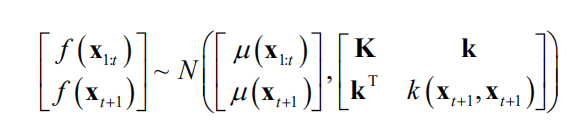
在这里 服从
维正态正态分布,其均值向量为
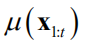
,协方差矩阵为 ,它们可以利用样本集
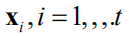
根据均值函数和协方差函数算出。 维列向量
根据
与
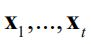
使用核函数计算
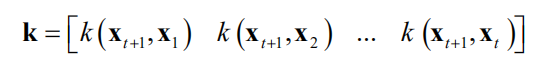
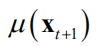
和
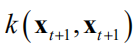
同样可以算出。在这里并没有使用到 的值,它们在计算新样本点的条件概率时才会被使用。
多维正态分布的条件分布仍为正态分布。可以计算出在已知
的情况下 所服从的条件分布,根据多维正态分布的性质,它服从一维正态分布
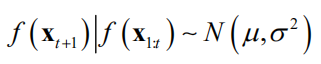
对于前面介绍的均值向量和协方差矩阵分块方案,根据多维正态分布条件分布的计算公式,可以计算出此条件分布的均值和方差。计算公式为
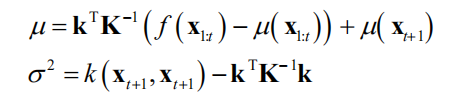
计算均值时利用了已有采样点处的函数值 。
的值是
与根据已有的采样点数据所计算出的值
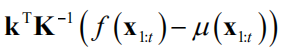
之和,与 有关。而方差
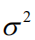
只与核函数所计算出的协方差值有关,与 无关。
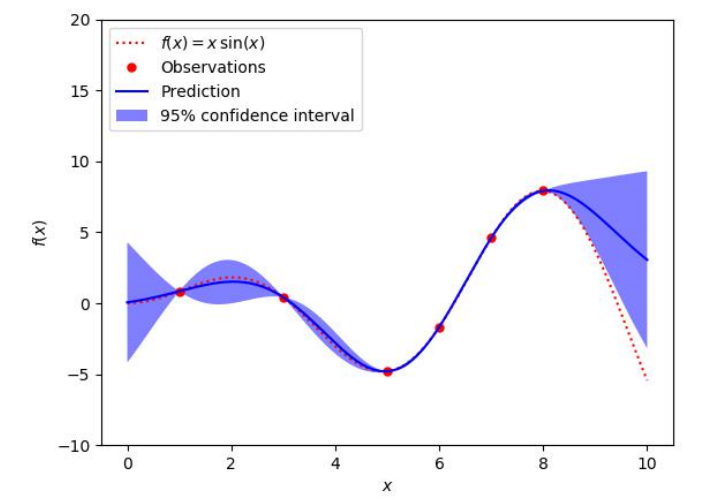
下面用一个例子说明高斯过程回归的原理,如图4所示。这里要预测的黑盒函数为
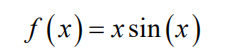
其图像是图4中的红色虚线。在这里我们并不知道该函数的表达式,只有它在5个采样点处的函数值,为图中的红色圆点。高斯过程回归根据这5个点处的函数值预测出了在 区间内任意点处的函数值
的概率分布。图中的蓝色实线是高斯过程预测出的这些点处的均值
。蓝色带状区域是预测出的这些点处的95%置信区间,根据该点处的均值 和方差
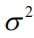
计算得到。
贝叶斯优化的思路是首先生成一个初始候选解集合,然后根据这些点寻找下一个最有可能是极值的点,将该点加入集合中,重复这一步骤,直至迭代终止。最后从这些点中找出函数值最大的点作为问题的解。由于求解过程中利用之前已搜索点的信息,因此比网格搜索和随机搜索更为有效。
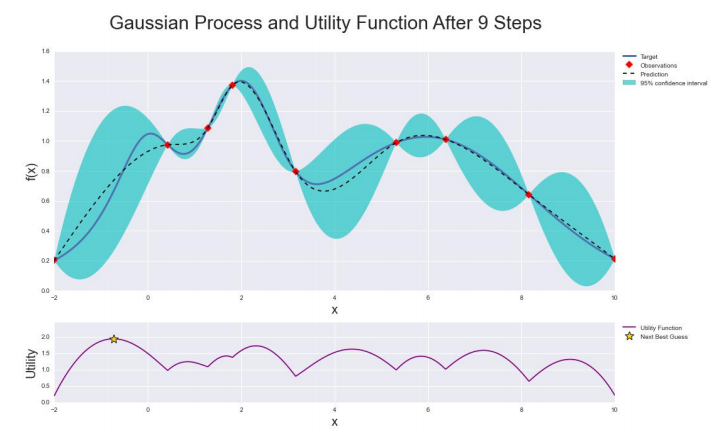
这里的关键问题是如何根据已经搜索的点确定下一个搜索点,通过高斯过程回归和采集函数实现。高斯过程回归根据已经搜索的点估计其他点处目标函数值的均值和方差,如图5所示。图5中蓝色实线为真实的目标函数曲线,黑色虚线为算法估计出的在每一点处的目标函数值。图中有7个已经搜索的点,用红色点表示。蓝色带状区域为在每一点处函数值的置信区间。函数值在以均值,即黑色虚线为中心,与标准差成正比的区间内波动。图5的下图为采集函数曲线,下一个采样点为采集函数的极大值点,以五角星表示。
在已搜索点处,黑色虚线经过这些点,且方差最小;在远离搜索点处方差更大。这也符合我们的直观认识,远离采样点处的函数值估计的更不可靠。根据均值和方差构造出采集函数,是对每一点是函数极值可能性的估计,反映了该点值得搜索的程度。该函数的极值点即为下一个搜索点。贝叶斯优化算法的流程如下所示。

其核心由两部分构成:
1. 高斯过程回归。计算每一点处函数值的均值和方差;
2. 根据均值和方差构造采集函数,用于决定本次迭代时在哪个点处进行采样。
算法首先初始化 个候选解,通常在整个可行域内均匀地选取一些点。然后开始循环,每次增加一个点,直至找到
个候选解。每次寻找下一个点时,用已经找到的
个候选解建立高斯回归模型,得到任意点处的函数值的后验概率。然后根据后验概率构造采集函数,寻找函数的极大值点作为下一个搜索点。接下来计算在下一个搜索点处的函数值。算法最后返回
个候选解的极大值作为最优解。
用已有采样点预测任意点处函数值的后验概率分布的方法在前面已经介绍,这里重点介绍采集函数的构造。采集函数用于确定在何处采集下一个样本点,它需要满足下面的条件。
1. 在已有的采样点处采集函数的值更小,因为这些点已经被探索过,再在这些点处计算函数值对解决问题没有什么用;
2. 在置信区间更宽的点处采集函数的值更大,因为这些点具有更大的不确定性,更值得探索;
3. 在函数均值更大的点处采集函数的值更大,因为均值是对该点处函数值的估计值,这些点更可能在极值点附近。
是一个随机变量,直接用它的数学期望
作为采集函数并不是好的选择,因为没有考虑方差的影响。常用的采集函数有期望改进(expected improvement),知识梯度(knowledge gradient)等,下面以期望改进为例进行说明。假设已经搜索了
个点,这些点中的函数极大值记为
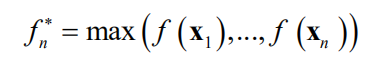
现在考虑下一个搜索点 ,我们将计算该点处的函数值
。如果
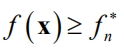
则这 个点处的函数极大值为
,否则为
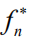
。对于第一种情况,加入这个新的点之后,函数值的改进为下面的正值
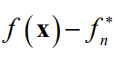
,对于第二种情况,则为0。借助于下面的截断函数
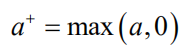
我们可以将加入新的点之后的改进值写成
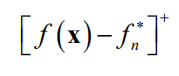
现在的目标是找到使得上面的改进值最大的 ,但该点处的函数值
在我们找到这个点
并进行函数值计算之前又是未知的。由于我们知道
的概率分布,因此我们可以计算所有
处的改进值的数学期望。并选择数学期望最大的
作为下一个探索点。因此可以定义下面的期望改进(expected improvement)函数
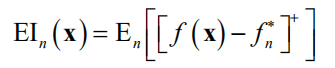
其中
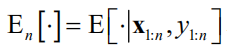
表示根据前面 个采样点
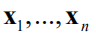
以及这些点处的函数值
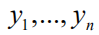
计算出的条件期望值。计算这个数学期望所采用的概率分布由高斯过程回归定义,是 的条件概率。
由于高斯过程回归假设 服从正态分布,可以得到数学期望的解析表达式。假设在
点处的均值为
,方差为
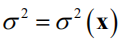
。令 ,根据数学期望的定义有
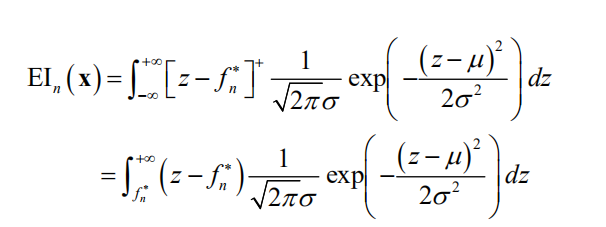
使用定积分的换元法,可以得到
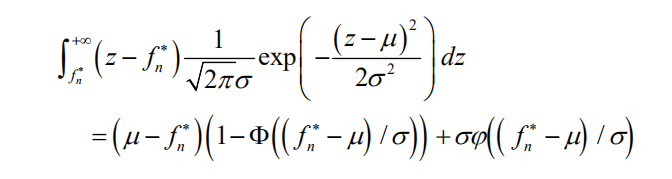
其中
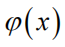
为标准正态分布的概率密度函数,
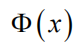
是标准正态分布的分布函数。如果令
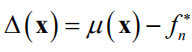
,则有
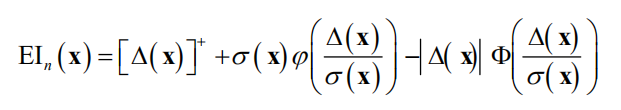
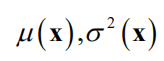
是 的函数,因此EI也是
的函数。具体的推导过程可以阅读2020年7-8月将在人民邮电出版社出版的《机器学习的数学》一书的第7章。
期望改进将每个点处的期望改进表示为该点的函数,下一步是求期望改进函数的极值以得到下一个采样点
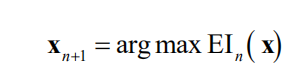
这个问题易于求解。由于可以得到目标函数的一阶和二阶导数,因此梯度下降法和L-BFGS算法都可以解决此问题。




