拓扑优化是一种强大的工具,通过使用这种工具,工程技术人员能够找到与其应用相关的问题的最佳解决方案。
瑞声达听力集团的客座作者 René Christensen 将带我们了解声学拓扑优化的重要性,以及如何在 COMSOL Multipysics 中应用声学拓扑优化。深入研究声学方面的拓扑优化,以及如何最优分配声介质来获得所需的响应。下面几个例子将进一步说明这种优化技术的潜力。
许多工程任务都围绕着优化某个应用程序的现有或未来设计而展开。对于改进设计来说,在特定行业内工作多年获得的最佳实践和经验至关重要。然而,优化问题往往非常复杂,以至于无法知道设计迭代是否朝着正确的方向发展。这就是优化 作为一门数学学科发挥作用的地方。
我们先回顾几个重要的术语。在优化中,无论是参数优化、形状优化,还是本例的拓扑优化,都至少有一个目标函数 。通常,我们希望将这个函数最小化。对于声学问题,我们可能希望将某一区域的声压降到最低,而对于结构力学问题,我们可能希望将结构某一部分的应力降到最低。我们将这一目标表述为
其中, 表示目标函数。设计变量
在整个优化过程中不断变化,从而得出最优解。它在标为
的设计域 内变化,该设计域通常不是整个有限元空间
,如下图所示。
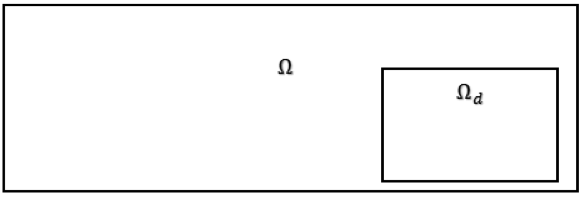
请注意,由于设计变量根据有限元离散化的设计域空间而变化,因此它是一个向量。对于这种特殊情况,我们将简单地将其作为变量来处理。
优化问题可能有多个目标函数,因此,工程技术人员需要决定每个目标应承载多大的权重。请注意,目标在优化过程中可能相互对立,因此在设置问题时应特别小心。
除目标函数外,通常还存在与优化问题相关的一些约束 。这些约束反映了相关问题的固有大小和/或权重限制。通过 COMSOL Multiphysics 中的 优化 接口,我们可以系统地输入设计变量、目标函数和约束条件。
通过使用拓扑优化,迭代过程中的设计变量在整个设计域内都是变化的。设计变量在整个域中是连续的,并且在域中取 0 到 1 之间的值:
理想情况下,我们希望设计变量的值接近 0 或 1。这样,就可以得到近似离散的设计,两种不同的(二元)状态界面清晰的分布在设计域中,这两种状态的描述将取决于与我们的优化相关的物理场。由于大多数文献都是在结构力学的背景下讨论拓扑优化,我们在下一节中将首先讨论这种物理场,并讨论它的声学对应物。
简要概述:研究 MBB 梁,目的是在给定载荷和边界条件下,通过将总应变能降至最低来使刚度最大化。设计域是整个有限元域的一部分。约束应用于结构的总质量。在设计空间中,杨氏模量通过设计变量 进行插值
为了帮助二元设计,我们可以使用固体各向同性材料罚函数(solid isotropic material with penalization,SIMP)插值法
其中
是罚因子,通常取 3 到 5 之间的值。通过使用这种插值法(以及密度的隐式线性插值),求解器避免了
的中间值,这些中间值提供的刚度重量比是我们不太想要的。我重新创建了上一篇文章中生成的 MBB 梁拓扑,如下所示。

图中,黑色表示用户定义的杨氏模量为 的材料。而白色对应于零刚度,表示不应该有材料。
我们继续讨论声学拓扑优化,这里我们使用声波在声介质中传播的频率相关解决方案。设计变量现在与声学物理场有关。我们的目标不是材料的二元空隙-材料 分布,而是实现二元空气-固体 分布,其中“固体”是指具有高密度、高体积模量的流体,用于模仿固体结构。
我们继续讨论声学拓扑优化,这里我们使用声波在声介质中传播的频率相关解决方案。设计变量现在与声学物理场有关。我们的目标不是材料的二元空隙-材料分布,而是实现二元空气-固体 分布,其中“固体”是指具有高密度、高体积模量的流体,用于模仿固体结构。
我们定义了四个参数来描述标准介质和“固体”介质的惯性和压缩特性:空气的密度为 ,体积模量为
,“固体”介质密度较大,为
,体积模量也较大,为
。在优化过程中,两种状态下设计域中的密度 和体积模量
因设计变量而有所不同——类似于我们的结构力学示例中杨氏模量的变化。但是声学分析需要不同的插值,使得相关值在设计变量为零时不趋于零,而是在空气和固体之间变化,因此
而
获得这些特性的最简单方法是在两个极值之间进行线性插值。这不一定是最好的方法,由于中间值 不会使用罚函数法,因此优化设计可能不是二元的。所以,无法实现制造,文献中给出了插值方案。在本文的案例中,我们使用的是材料属性合理近似(RAMP)插值法(见参考文献 1)。
和结构优化一样,我们定义了一个设计域,从中可以进行材料分配,同时满足约束条件。可以通过设计变量定义面积和体积约束。例如,设计域上的面积约束可以表示为不等式约束
其中, 是指定实体属性的设计域与整个设计域的面积比。
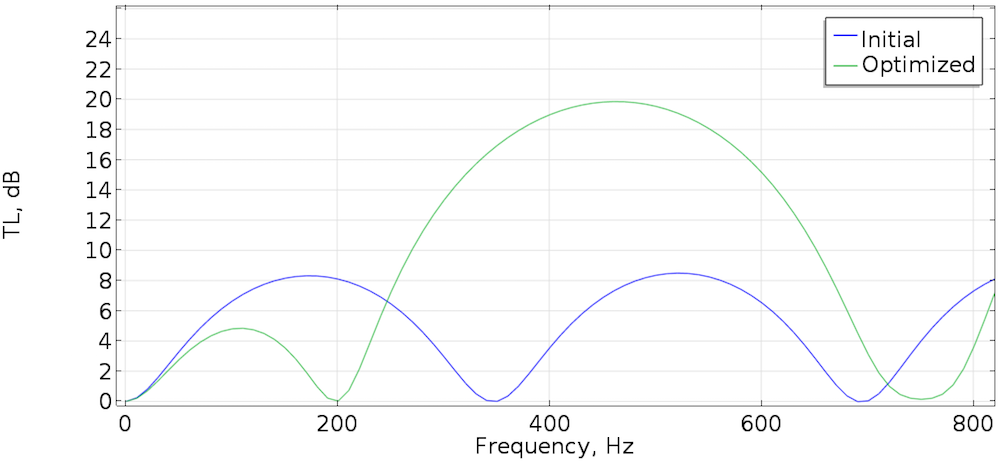
我们先来看一个消声器的例子。为简单起见,我们只在二维域中执行相关操作。描述消声器特征使用的典型测量方法是传输损耗,以 TL 表示,它是功率输入相对于功率输出的度量:
传输损耗用所谓的三点法计算(见参考文献 2),我们使用计算的传输损耗作为目标函数,尝试在单一频率(本例中为 420 Hz)下将该函数最大化:
管状截面的上方和下方定义了两个设计域,这些域受到限制,二维区域最多有 5% 是结构,因此其中 95% 肯定是空气:
设计域的初始状态为 100% 空气,即 =0。下面的动画显示了从初始状态到最终拓扑形态的演变。
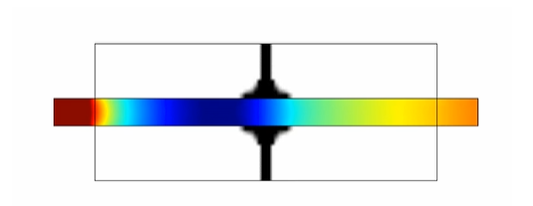
优化结构采用“双膨胀室”(见参考文献 3)消声器拓扑结构。传输损耗在目标频率下增加了约 14 分贝,如下图所示。然而,在目标频率之外的所有频率下,传输损耗也发生了变化,这对于特定应用来说可能非常重要。因此,单频优化可能不是典型设计问题的最佳选择。
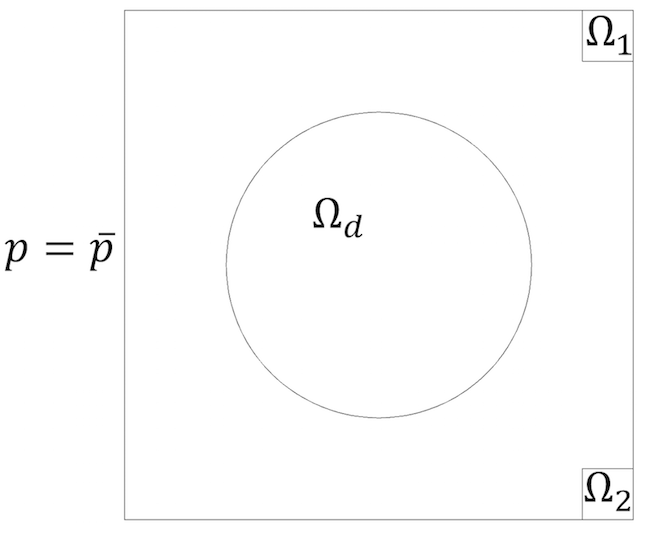
下面我们探讨如何优化两个目标函数和两个频率。这里,我们再次设想一个有三面硬墙的二维房间,在房间的左侧有一个压力输入。房间还包含两个目标区域: 和
,分别位于房间右侧的两个角落。两个目标如下:
- 将频率
下的声压级降至最低,并
- 将频率
下的声压级降至最低
其中包含圆形设计域 和 10% 结构的面积约束。初始状态为
=0,使得设计域 100% 为空气。
由于存在多个目标函数,我们必须对不同目标的相对权重或重要性做出选择。本例中,两个目标同等重要,我们将问题描述为最小-最大问题:
下图显示了使用相同压力尺度的两种频率下的优化拓扑(蓝色)和声压。请注意优化的拓扑如何在第一个频率下导致右上角出现低压区(绿色)。同时,这种优化的拓扑确保在第二个频率下右下角出现类似的低压区。如果只能采用反复试验法,这无疑是一项极具挑战的任务。
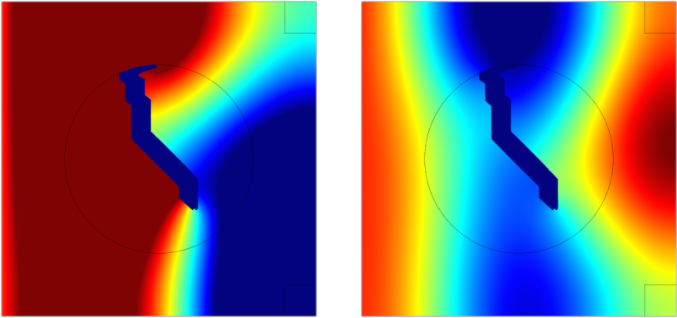
频率 (左)和频率
(右)下的声压。优化的拓扑以蓝色显示。
第三个也是最后一个示例,我们将在一个频率范围内优化单个目标。声源被辐射到二维域,该二维域中最初有一个圆柱形声场,并有两个正方形设计域,但由于对称性,我们在仿真中只考虑一半的几何结构。本例中,我们希望声源前方 0.4 米处的轴上声压 保持恒定。优化在 4000 到 4200 Hz(50 Hz 步长,总共五个频率)的频率范围内进行。我们可以通过 COMSOL Multiphysics 中的“全局最小二乘目标”功能来实现这一点,问题表述为:
初始状态仍为 =0。优化的拓扑以及初始状态和优化状态的声场如下所示。
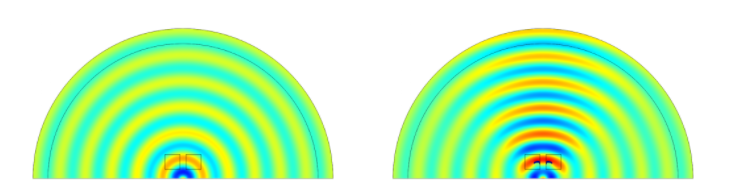
4 kHz 下初始状态(左)和优化状态(右)的声压,优化的拓扑在方形设计域中以蓝色显示。
由于初始状态观测点中的声压级低于目标压力,因此拓扑优化产生反射器来聚焦轴上声音。优化前后的声压级如下图所示。在优化后的频率范围内,压力大小接近期望的目标压力。
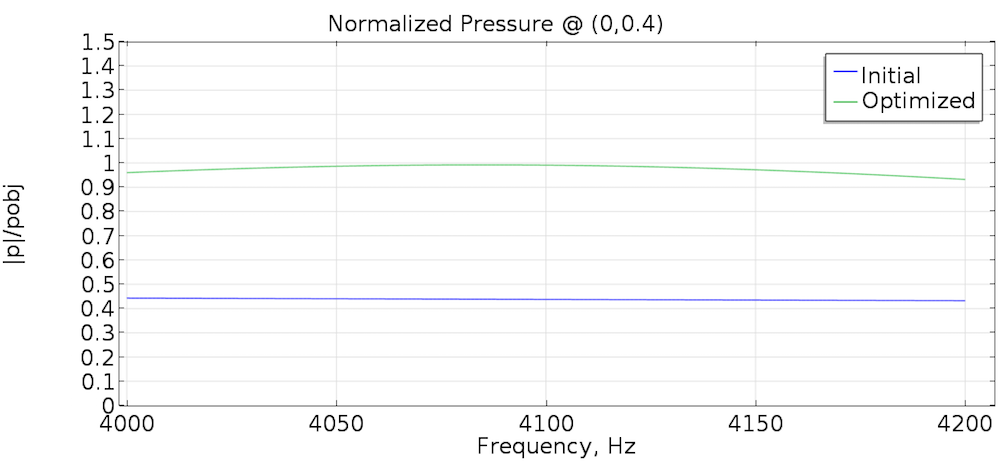
初始状态和拓扑优化后的压力大小除以 。
声学拓扑优化为帮助声学工程技术人员实现创新设计提供了巨大的潜力。正如我今天演示的,你可以在 COMSOL Multiphysics 中有效地使用这项技术。通过适当地表述目标和约束条件,可以构建具有全新和创新拓扑结构的应用程序,用传统方法很可能找不到这些拓扑结构。
我要特别感谢丹麦技术大学(Technical University of Denmark)的副教授 Niels Aage 就优化这一主题进行的多次富有成效的讨论。
要了解更多关于在 COMSOL Multiphysics 中使用声学拓扑优化的信息,建议你从我们的“案例下载”页面下载以下示例:
房间二维模型中声学模态的拓扑优化与验证- M.P. Bendsoe, O. Sigmund, Topology Optimization: Theory, Methods, and Applications, Springer 2003.
- T.W. Wu, G.C. Wan, Muffler, “Performance studies and using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss”, Trans. ASME: J. Vib. Acoust. 118 (1996) 479-484.
- Z. Tao, A.F. Seybert, “A review of current techniques for measuring muffler transmission loss”, SAE International, 2003.
René Christensen 在振动声学领域工作了十余年,既担任顾问(iCapture ApS),也是助听器行业的工程技术人员(Otion A/S,瑞声达听力集团)。他对微声学中的热粘性效应建模特别感兴趣,这也是他博士学位的课题。René 于 2015 年加入瑞声达听力集团的硬件平台声学研发团队,担任高级声学工程师,他在这个职位上致力于助听器的设计和优化。




