机器(深度)学习求解组合优化问题综述_耀世娱乐-耀世注册登录官方入口

主要是参考以下三篇文章：

组合优化问题(Combinatorial Optimization Problem, COP)是一类在离散状态下求极值的最优化问题，数学模型为：

$\\\\\\begin{array}{l}\\min F(x)\\\\ s.t. G(x)\\geq0\\\\ x\\in D\\end{array}$

其中 $x$ 为决策变量， $F(x)$ 为目标函数， $G(x)$ 为约束条件， $D$ 表示离散的决策空间，为有限个点组成的集合。

组合优化的主要目标是设计出解决这类问题的有效算法。在计算机科学中，只要算法的基本步骤数在输入的大小上增长为多项式，算法就被称为“有效的”。

P问题：可以用确定性算法在多项式时间内解决的问题，然而大多数组合优化问题没有精确的多项式时间算法；
NP问题：不能确定能否在多项式时间内找到解，但是可以在多项式时间内验证解是否正确。
NP-complete(NPC)问题：它是一个NP问题，同时所有的NP问题都能在多项式时间内约化到它。如果这种问题如果存在多项式时间的算法，那么所有NP问题都是多项式时间可解的；
NP-hard问题：所有NP问题都能在多项式时间内约化到它，但它不一定是一个NP问题，许多组合优化问题是NP-hard的。

(1) 背包问题 (Knapsack Problem, KP)

背包问题涉及一个具有有限容量 $W$ 的背包以及一个具有 $n$ 个物品的集合 $O=\\{o_1, o_2,\\dots,o_n\\}$ ，其中每件物品 $o_j$ 都有一个重量 $w_j\\leq W$ 和一个价值 $p_j$ ，不失一般性，假设 $W,w_j,p_j\\in Z^+,j=1,...,n$ 且 $\\sum_{j=1}^nw_j>W$ 。可行解集合 $F$ 由物品子集 $f$ 组成， $f$ 中的物品总重量不超过 $W$ ，最大化目标函数为 $c(f)=\\sum_{j\\in f}p_j$ 。

(2) 旅行商问题 (Travelling Salesman Problem, TSP)

TSP问题由一组城市定义，目标是找到只访问每个城市一次并返回起点的最短(耗费最小)的路线。TSP问题定义在一个无向边权图 $G=\\langle V,E\\rangle$ 上， $w(e)$ 是边 $e\\in E$ 的权重，可行解集合 $F$ 由构成哈密顿圈的边的子集 $f$ 构成，最小化目标函数 $c(f)=\\sum_{e\\in f}w(e)$ 。

(3) 车辆路径问题 (Vehicular Routing Problem, VRP)

VRP问题是TSP问题的一个推广，目标是找到访问所有节点(城市)的最佳路线，使得总成本(路线长度、时间、或车辆数量等)最小化，同时保证所有其他约束(如容量)被满足。基本形式中，每个节点只被一辆有限容量的车访问一次。给定一个完全图 $G=\\langle V,E\\rangle$ ，其中一个节点 $v\\in V$ 是depot，其余为待访问节点。边权重 $w(e)$ 反映cost。每个节点有一个需求，并且车辆的容量至少与节点需求一样大。

(4) 极大团问题 (Maximal Clique, MC)

给定无向图 $G=\\langle V,E\\rangle$ ，目标是找到一个最大的节点子集构成团。 $G$ 的一个团是 $G$ 的一个完全子图。

(5) 最大割问题 (Maximum Cut, MaxCut)

给定一个无向图 $G=\\langle V,E\\rangle$ ，边 $(i,j)\\in E$ 有非负边权， $w_{ij}=w_{ji}\\geq0$ 。目标是找到节点子集 $S\\subseteq V$ ，从而最大化割 $(S,\\bar{S})$ 中边的权重， $\\max w(S,\\bar{S})=\\sum_{i\\in S,j\ otin S}w_{ij}$ 。

(6) 最小顶点覆盖 (Minimum Vertex Cover, MVC)

给定无向图 $G=\\langle V,E\\rangle$ ，找到最小节点子集 $V_c\\subseteq V$ ，使得图中每条边 $e\\in E$ 都与 $V_c$ 中至少一个节点相关联。(最小顶点覆盖对应于最大独立集的补集)

(7) 最大独立集 (Maximal Independent Set, MIS)

给定无向图 $G=\\langle V,E\\rangle$ ，找到最大节点子集 $U\\subseteq V$ 使得 $U$ 中任意两点之间没有边相连，即对于 $U$ 中的节点对 $(u_i,u_j)$ ， $(u_i,u_j)\ otin E$ 。

(8) 最大覆盖问题 (Maximum Coverage Problem, MCP)

给定一组集合 $\\mathcal{U}=\\{S_n\\}_{n=1}^m$ 和一个数 $k$ ，从 $\\mathcal{U}$ 中选择至多 $k$ 个集合 $S_{i_1},S_{i_2},...,S_{i_k}$ ，使得覆盖元素的数量，即集合并集的基数 $|\\cup_{j=1}^kS_{i_j}|$ 最大。budget版本：给定一个二部图， $V=V_1\\cup V_2$ ，以及budget $b$ ，选择一个节点子集 $S\\subseteq V_1$ ， $|S|=b$ ，使得至少一个邻居来自 $S$ 的 $V_2$ 中的节点数最大。

(9) 可满足性问题 (Satisfiability Problem, SAT)

考虑一个布尔逻辑表达式，它由布尔变量、括号以及运算符(AND、OR、NOT)组成。SAT问题就是要找到所有变量的布尔赋值，使得表达式为真，或证明不存在这样的赋值。

方法	举例	优缺点
精确算法	分支定界法、动态规划法	优点：能够得到问题的精确解。缺点：问题规模扩大时，该类算法将消耗巨大的计算量，难以扩展到大规模问题。
近似算法	贪心算法、局部搜索算法、线性规划、松弛算法、序列算法	优点：在可接受的时间内得到一个近似最优解，能够对解的质量提供理论保证。缺点：当问题规模很大时，仍然会导致较大的计算耗时。
启发式算法	模拟退火算法、禁忌搜索、进化算法(遗传算法、差分进化算法等)、蚁群优化算法、粒子群算法、迭代局部搜索、变邻域搜索	优点：比精确算法、近似算法速度快。缺点：对解的质量没有保证。

A. 注意力机制[Attention Mechanisms]

循环神经网络(Recurrent Neural Network, RNN)是用于处理序列数据的神经网络。RNN通过以下迭代求解方程从输入序列 $(x_1, x_2, ...,x_T)$ 计算输出序列 $(y_1,y_2,...,y_T)$ ：

$h_t=f(x_t,h_{t-1})=f(W^{hx}x_t+W^{hh}h_{t-1}+b^h)\\\\ y_t=\\sigma(W^yh_t+b^y)$

其中 $h_t$ 表示第 $t$ 步的隐藏单元， $W^{hx},W^{hh},W^y$ 是所有RNN单元共享的权重矩阵， $b^h,b^y$ 是偏置， $f$ 是非线性激活函数。但当处理的序列较长时，RNN中较远时间步会出现梯度消失的问题。可以使用LSTM或GRU来克服这个问题。

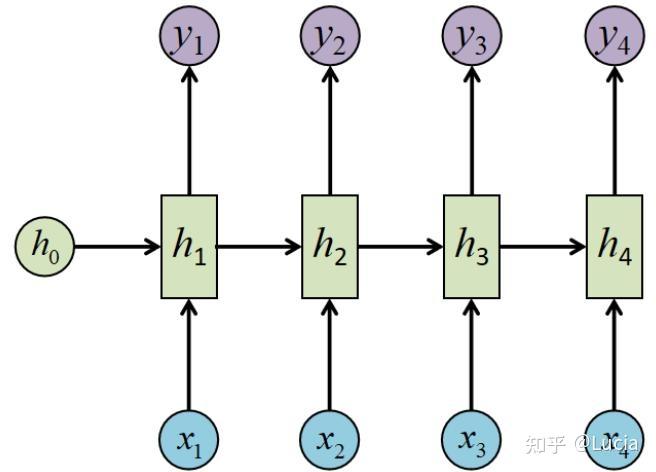
RNN模型中输入输出序列具有相同的长度，而Sequence-to-Sequence模型允许输入和输出序列有不同的长度。Seq2Seq模型是基于两个RNN(一般是LSTM)的Encoder-Decoder结构。第一个RNN将输入序列映射到一个固定大小的向量，然后第二个RNN将这个向量再映射到输出序列。这种方法中可变输入序列必须被压缩成一个固定长度的向量，当输入序列比训练期间观察到的序列长时，可能会降低模型的预测性能。

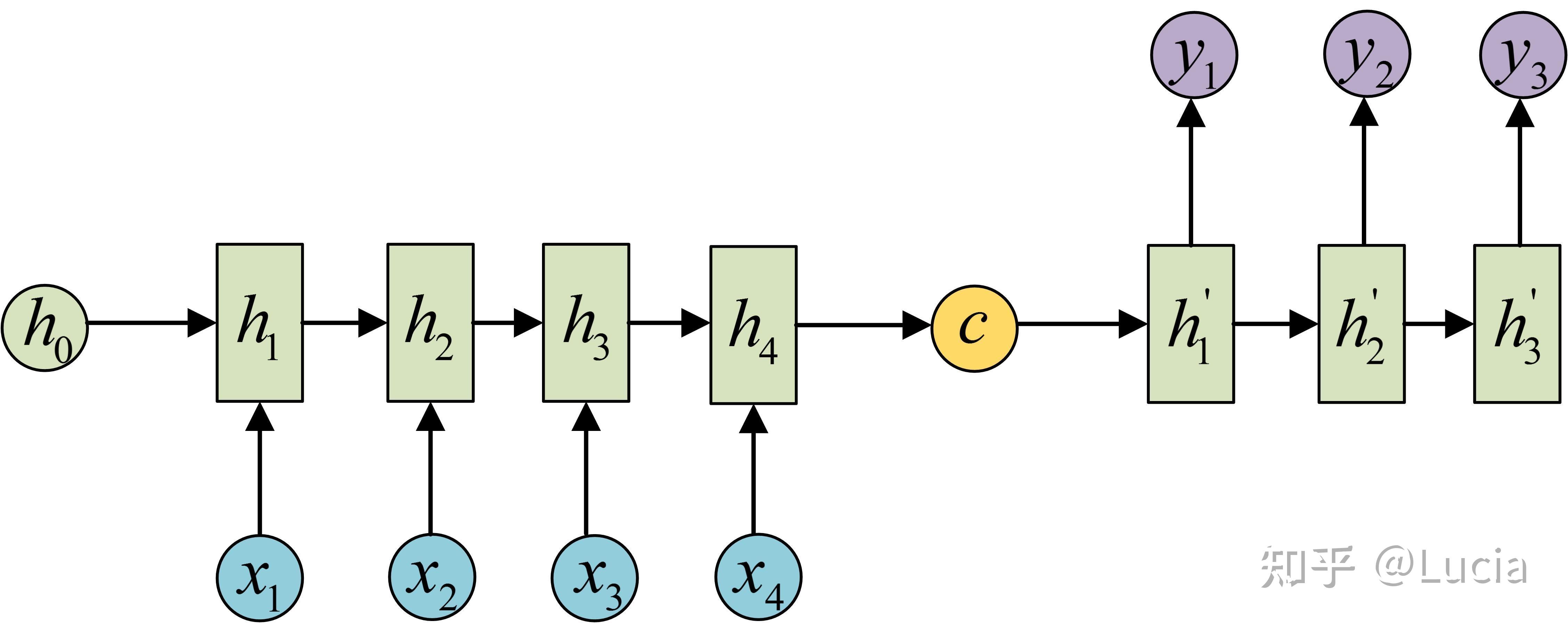
注意力机制(Attention Mechanisms)已经成为解决上述Encoder-Decoder架构局限性的一种方法。注意力机制允许Decoder使用Encoder的任何隐藏状态，而不是使用Encoder在输入序列末尾(Encoder的最后隐藏状态)产生的固定长度向量。记Encoder和Decoder的隐藏状态分别为 $(e_1,e_2,...,e_n)$ 和 $(d_1, d_2, ...,d_m)$ ，任一时刻 $i$ 的注意力向量计算为Decoder状态和所有Encoder状态之间的相似性：

$\\\\\\begin{array}{ll}u_j^i=f(W_1e_j+W_2d_i),&j\\in(1,...,n)\\\\ a_j^i=softmax(u_j^i),&j\\in(1,...,n)\\\\ c_i=\\sum_{j=1}^na_j^ie_j, \\end{array}$

context向量 $c_i$ 由Encoder状态按照注意力分数加权求和得到，之后将向量 $c_i$ 和Decoder状态 $d_i$ 进行拼接或加和得到的向量用于预测和计算下一步Decoder的隐藏状态。这种预测方法比Seq2Seq模型效果更好。

模型通过最大化给定参数 $\ heta$ 和输入序列 $\\mathcal{P}=(P_1,...,P_n)$ 选择最优输出序列 $\\mathcal{C}^\\mathcal{P}$ 的条件概率来训练参数：

$\\\\\ heta^*=\\arg\\max_\ heta\\sum_{\\mathcal{P},\\mathcal{C}^\\mathcal{P}}\\log p(\\mathcal{C}^\\mathcal{P}|\\mathcal{P},\ heta)$

一旦学习了模型的参数 $\ heta^*$ ，就可以利用它们进行推断：给定一个输入序列 $\\mathcal{P}$ ，选择概率最大的输出序列 $\\hat{\\mathcal{C}}^\\mathcal{P}=\\arg\\max_{\\mathcal{C}^\\mathcal{P}}p(\\mathcal{C}^\\mathcal{P}|\\mathcal{P},\ heta^*)$ 。
另一个基于注意力机制的新发展是Transformer，它也是一个Encoder-Decoder结构。它与其他注意力框架的本质不同之处在于，RNN被具有位置编码的一堆自注意力层所取代，这些自注意力层是用全连接层的神经网络来实现的。

首先，通过将输入乘以三个不同的权重矩阵，以三种不同的方式(Key, Value, Query)表示输入。然后，计算Query和所有Key的点积，在应用softmax函数后，获得Value的权重，输出就是Value的加权求和。

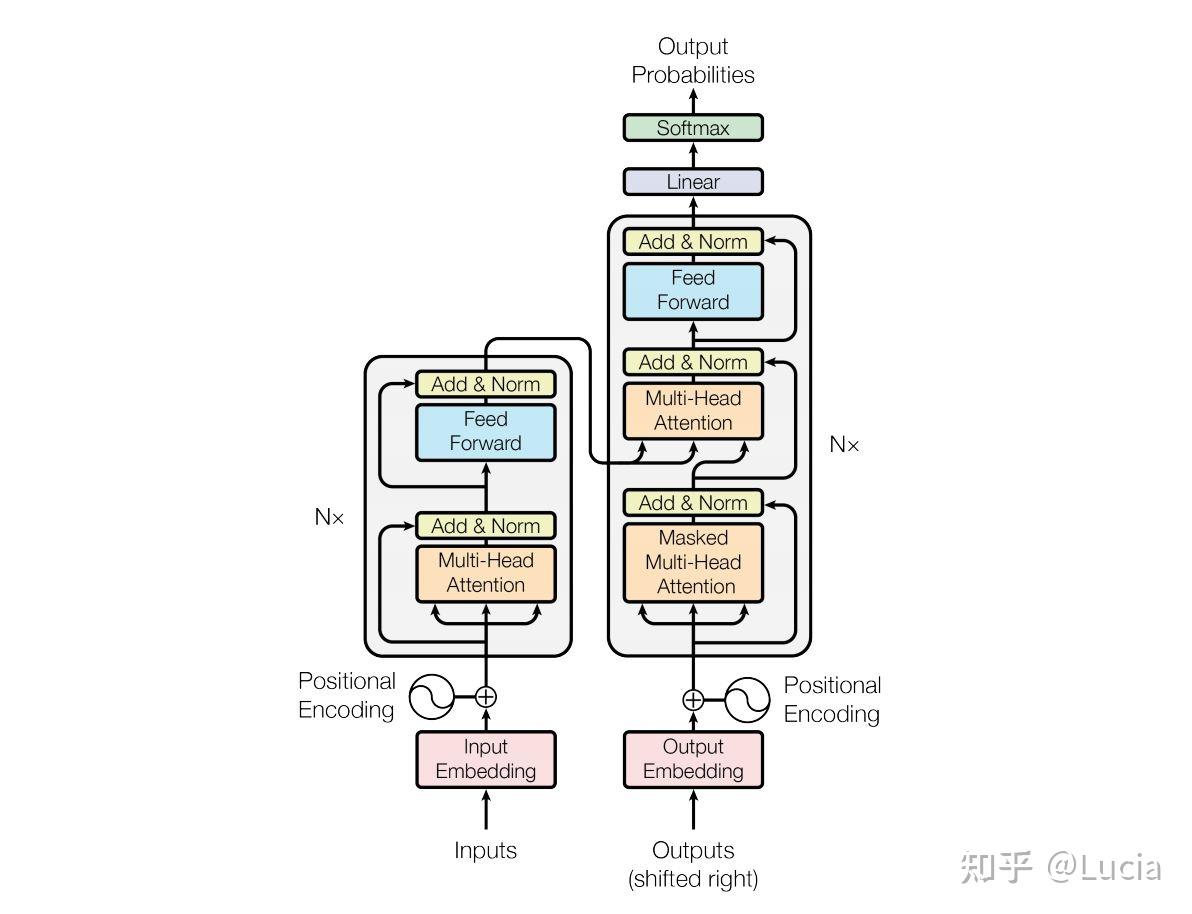
$\\\\Attention(Q,K,V)=softmax(\\frac{QK^\ op}{\\sqrt{d_k}})V$

B. 图神经网络[Graph Neural Networks]

图神经网络的基本思想是通过更新节点的状态来有效地捕获单个节点之间的(通常是复杂的)交互。在GNN模型中是通过与相邻节点交换信息(节点嵌入)来周期性地更新节点的隐藏状态，直到达到稳定的平衡：

$\\\\h_v^{(t)}=\\sum_{u\\in\\mathcal{N}(v)}f(x_v,x^e_{(v,u)},x_u,h_u^{(t-1)})$

其中节点embedding是随机初始化的， $f()$ 是任意可微函数且是一个压缩映射，这样会保证节点的embedding收敛。一旦达到收敛，节点隐藏状态就被发送到read-out层。

GGNN模型通过使用GRUs和反向传播来扩展和修改GNN框架，这消除了重复更新节点状态直至收敛的需要。该框架的一些优点是：节点embedding可以通过节点特征初始化，并且可以使用中间输出。更新公式为：

$\\\\h_v^{(t)}=GRU(h_v^{(t-1)},\\sum_{u\\in\\mathcal{N}(v)}Wh_u^{(t-1)})$

GCN模型将卷积运算推广到图数据，从图数据中提取特征。它层与层之间的计算公式为：

$\\\\H^{(l+1)}=\\sigma(\ ilde{D}^{-1/2}\ ilde{A}\ ilde{D}^{-1/2}H^{(l)}W^{(l)})$

其中 $\ ilde{A}=I+A$ ， $A$ 是图的邻接矩阵， $\ ilde{D}_{ii}=\\sum_j\ ilde{A}_{ij}$ ， $W^{(l)}$ 是权重矩阵。

图神经网络可以分为两类：谱方法和空间方法。前者源于图信号处理，并使用滤波器来定义卷积，后者采用信息传递思想。

MPNN模型是基于空间方法图神经网络的一个通用框架，将基于空间的图神经网络看作是一个消息传递过程，在这个过程中，信息通过连接节点的边在节点之间交换。消息传递函数为：

$\\\\h_v^{(k)}=u_k(h_v^{(k-1)},\\sum_{u\\in\\mathcal{N}(v)}m_k(h_v^{(k-1)},h_u^{(k-1)},x_{vu}^e))$

其中 $k$ 是层索引， $u$ 表示更新函数， $m$ 是消息传递函数，节点的隐藏表示可以被传递到输出层，或传递到read-out函数以产生整个图的有用表示。

注意力机制也已经被结合到图神经网络中，GAT模型每层的输入是节点的特征，输出更新的节点特征，这些输出的节点特征通过以注意力机制为核心的聚合操作实现：

$\\\\\\begin{array}{l}\\alpha_{ij}=\\frac{\\exp(LeakyReLU(\\vec{a}^\ op[W\\vec{h}_i||W\\vec{h}_j]))}{\\sum_{k\\in\\mathcal{N}_i}\\exp(LeakyReLU(\\vec{a}^\ op[W\\vec{h}_i||W\\vec{h}_k]))}\\\\ \\vec{h}_i'=\\sigma(\\sum_{j\\in\\mathcal{N}_i}\\alpha_{ij}\\vec{h}_j) \\end{array}$

Graph Embedding学习高维图数据的低维向量表示，旨在保留图结构和节点内容信息，学习到的低维向量表示可用于后续的任务。

C. (深度)强化学习[(Deep) Reinforcement Learning]

强化学习是基于交互的面向目标的学习，因此在概念上不同于其他两种主要且流行的机器学习方法:监督和无监督。强化学习从与(不确定的)环境交互中学习(而不是像在有监督的情况下那样由标记数据集指导)，目标是最大化奖励函数(而不是像在无监督的情况下那样找到隐藏的模式)。此外，强化学习实现了探索机制，而这在另外两种方法中是不存在的。

强化学习的四个要素：

策略(Policy)：某一时刻，Agent在不同状态(state)下如何选择动作(action)；
奖励(Reward)：Agent在每个时间步采取动作后得到环境的一个反馈值；
值函数(Value Function)：从一个状态开始一直执行下去，能够得到的总奖励的期望值。
环境模型(Model of the Environment)：描述马尔可夫决策过程的五元组，给定一个状态和动作，模型会预测这个动作导致的下一个状态和奖励。

马尔可夫决策过程：是一个基本的数学模型 $M$ ，用于分析表示系统(Agent)于环境 $M=\\langle S,A,T,R,\\gamma\\rangle$ 之间的相互作用，定义为：

状态空间 $S$
动作集合 $A$
转移模型 $T:S\ imes A\\rightarrow S, s_{t+1}=T(s_t,a_t)$
奖励函数 $R:S\ imes A\\rightarrow\\mathbb{R}, R_{t+1}=R(s_t,a_t)$
折扣因子 $0\\leq\\gamma\\leq1$

回报(Return)定义为： $G_t=\\sum_{i=0}^\\infty\\gamma^iR(s_{t+i},a_{t+i})$ 。

目标可以表示为： $\\max_\\pi G_t$ 使得 $s_{t+1}=T(s_t,\\pi(s_t))$ 。

强化学习主要有两大类方法：表格解法(Tabular Methods)和近似解法(Approximate Solution Methods)。

Tabular Methods

当状态空间和动作集合足够小时，近似值函数可以表示为表格，这种方法通常能够找到精确最优解和最优策略。

策略 $\\pi$ 是从状态空间到动作集合的映射 $\\pi:S\\rightarrow A$ 。值函数 $v_\\pi:S\\rightarrow\\mathbb{R}$ 为每个状态 $s\\in S$ 分配一个值 $v_\\pi\\in\\mathbb{R}$ 。当从状态 $s$ 开始并按照策略 $\\pi$ 执行， $v_\\pi$ 被计算为预期回报：

$\\\\v_\\pi(s_t)=\\mathbb{E}\\left[\\sum_{i=0}^\\infty\\gamma^iR(s_{t+i},\\pi(s_{t+i}))|s_t=s\\right]$

类似地，可以定义动作值函数 $q_\\pi$ ，该函数考虑处于状态 $s$ 时采取动作 $a$ 并按照策略 $\\pi$ 执行往后的时间步的回报：

$\\\\q_\\pi(s_t,a_t)=R(s_t,a_t)+\\mathbb{E}\\left[\\sum_{i=0}^\\infty\\gamma^iR(s_{t+i},\\pi(s_{t+i}))|s_t=s,a_t=a\\right]$

值函数总是遵循Bellman方程：

$\\\\v_\\pi(s)=R(s,\\pi(s))+\\gamma v_\\pi(T(s,\\pi(s)))$

最优策略 $\\pi^*$ 的值函数是所有可能策略的最大值：

$\\\\v_*(s):=\\max_\\pi v_\\pi(s)$
被称为最优值函数(optimal value function)。同样最佳动作值函数为：

$\\\\q_*(s,a):=\\max_\\pi q_\\pi(s,a)$

这两者可以通过以下方式联系在一起：

$\\\\v_*(s)=\\max_{a\\in A}q_*(s,a)$

最优值函数的递归关系：

$\\\\v_*(s)=\\max_{a\\in A}\\left[R(s,a)+\\gamma v_*(T(s,a))\\right]$

被称为Bellman最优方程。

当转移函数未知时，Bellman方程的解可以通过迭代过程找到。基于这一事实，提出了Q-Learning算法。Q-Learning算法创建一个由状态和动作所有可能组合组成的Q-table，Agent根据采取动作时收到的奖励更新表中的条目，Q-table中的值反映累计奖励。然而，在现实场景中，Q-table会变得非常大，不可行。为了克服这样的挑战，提出了一种基于Q-Learning和深度神经网络的算法，称为深度Q网络(Deep Q-Network, DQN)。DQN是使用一个深度网络来拟合Q-table，使用端到端强化学习来学习最优策略。

Approximate Solution Methods

在任意大的状态空间中，即使在无限时间和数据的假设下，寻找最优策略也是不实际的，并且常常是不可行的，最好采用近似解。REINFORCE是一种近似的策略梯度方法，又称基于蒙特卡洛的策略梯度方法。它定义从状态 $s$ 开始并遵循策略 $\\pi$ 执行后续步骤的总回报为 $J(\ heta)$ ，然后通过 $J(\ heta)$ 相对于 $\ heta$ 的梯度来学习参数化策略。具体分为三个步骤：(1)执行策略 $\\pi$ ，(2)计算优化目标的梯度 $\ abla_\ heta J(\ heta)$ ，(3)相应地调整参数值 $\ heta\\leftarrow\ heta+\\alpha\ abla_\ heta J(\ heta)$ 。 $J(\ heta)$ 的梯度计算公式中一般会减去一个策略的平均表现(baseline)，如果当前策略的表现比”平均”好, 则对该策略进行正向激励, 反之亦然。

Actor-critic Methods

Actor-critic方法是一种混合方法，它融合了value-based和policy-based的方法的优点。

Value-based方法：(例如DQN) 评估最优累积奖励，旨在通过获得最优值函数或最优动作值函数来找到最优策略 $\\pi$ ；
Policy-based方法：(例如REINFORCE) 旨在通过优化代表策略的参数函数(通常是神经网络)来直接估计最佳策略。

Actor-critic方法中，使用策略函数负责选择动作并与环境交互的为actor，使用值函数评估actor的表现，指导actor下一步选择动作的为critic。

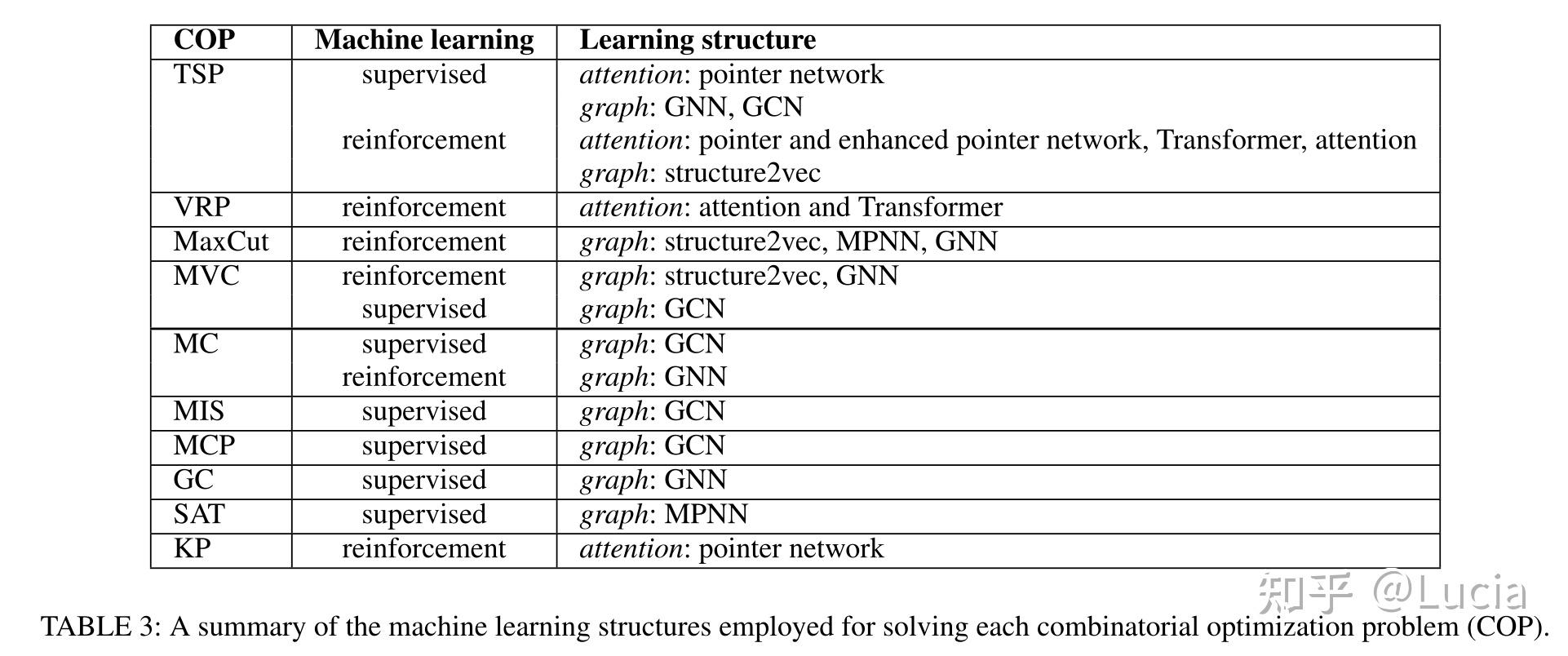
!!! 汇总的表格在最后 !!!

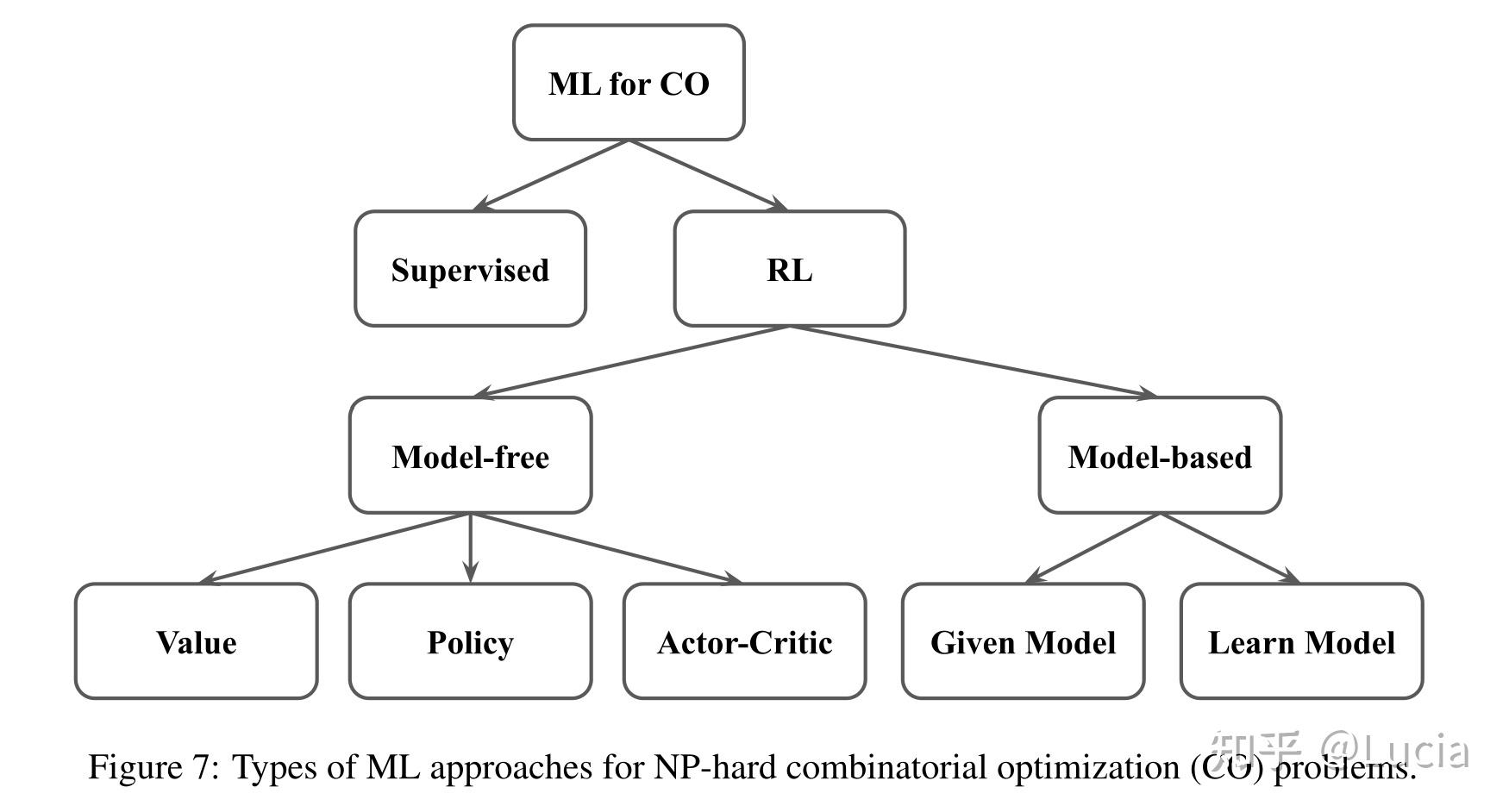
组合优化问题的机器学习方法首先是基于深度神经网络类型——注意机制、GNN及其变体分类，然后在每个类别中，分为监督学习方法以及强化学习方法。

A. 注意力机制：Pointer Networks和Transformer架构

监督学习方法

前面提到的Seq2Seq模型要求输出序列的长度事先固定，这个框架不能应用于具有依赖于输入长度的可变输出的组合优化问题。所以Vinyals等人提出了Pointer Network模型来解决组合优化问题。

Pointer Network核心思想是利用Encoder对组合优化问题的输入序列进行编码得到特征向量, 再利用Decoder结合Attention计算方法以自回归的方式逐步构造解, 自回归即每次选择一个节点, 并在已选择节点的基础上选择下一个节点, 直到构造得到完整解。经典Pointer Network模型的Encoder和Decoder均为LSTM，以TSP问题为例：

首先将每个城市的二维坐标转换成高维的节点表征向量 $s_i$ ，Encoder依次读入各个城市的 $s_i$ ，最终编码得到一个存储输入序列信息的向量Vector，同时计算得到每个城市的隐藏状态 $e_i$ 。

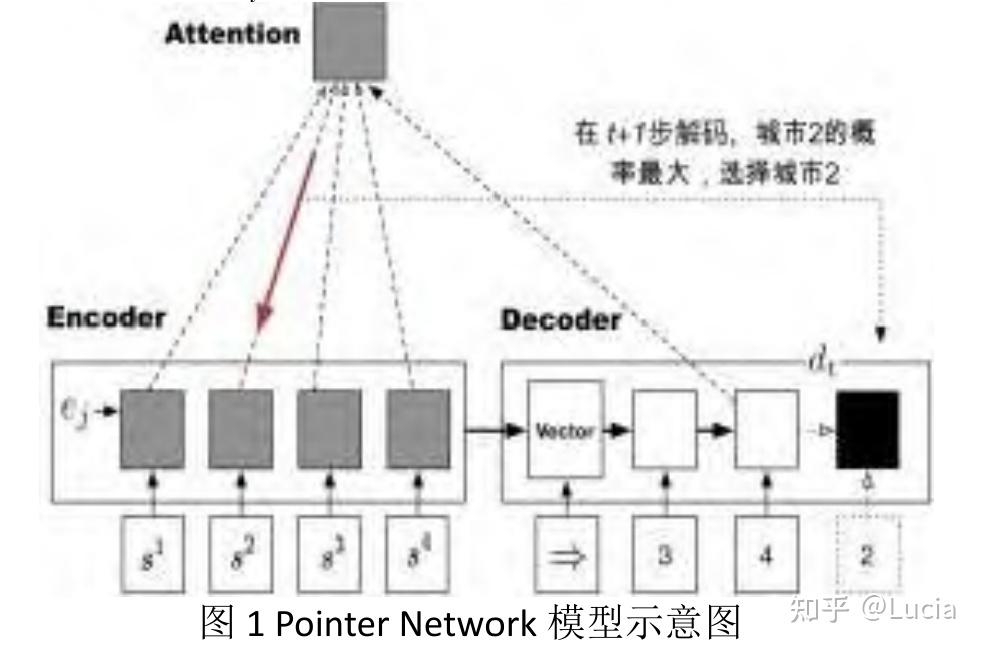
然后Decoder对Vector进行解码，每一个时间步利用Attention机制根据当前步的Decoder隐藏状态 $d_t$ 和Encoder得到的各个城市的隐藏状态 $e_j$ 计算选择各个城市的概率，可选择概率最大的节点作为下一步选择的城市，计算公式为：

$u_j^t=v^\ op\ anh(W_1e_j+W_2d_t),j\\in(1,...,n)\\\\ a=softmax(u^t)$

Vinyals等人提出的Pointer Network模型采用监督学习方法，需要提供大量的最优路径的标签数据集，实际应用较为困难，而且模型的性能是由标签的质量决定的，永远不会超过标签解的质量。为了克服这些限制，目前的研究中通常以强化学习算法对模型参数进行训练。

强化学习方法

强化学习通过试错机制不断训练得到最优策略，首先需要将组合优化问题建模为马尔科夫过程，其核心要素为状态、动作以及反馈。以 TSP 问题为例，其问题的状态为城市的坐标 $s$ 以及已经访问过的城市，动作为第 $t$ 步选择的城市 $\\pi_t$ ，所有动作组成的城市访问顺序 $\\pi$ 即为组合优化问题的解，反馈 $r$ 是路径总距离的负数，即最小化路径长度，策略即为状态 $s$ 到动作 $\\pi$ 的映射，策略通常为随机策略，即得到的是选择城市的概率 $p_\ heta(\\pi|s)$ , 该随机策略建模为：

$\\\\p_\ heta(\\pi|s)=\\prod_{t=1}^np_\ heta(\\pi_t|s,\\pi_{1:t-1})$

该随机策略可以建模为上节所述的指针网络模型，其参数为 $\ heta$ 。

由于TSP问题的优化目标是最小化总的路径长度 $L(\\pi)$ ，而REINFORCE也是以总反馈作为参数更新的标准，因此现有的研究中通常采用REINFORCE强化学习算法对策略的参数 $\ heta$ 进行训练优化，总反馈即为路径总长度的负数 $-L(\\pi)$ 。

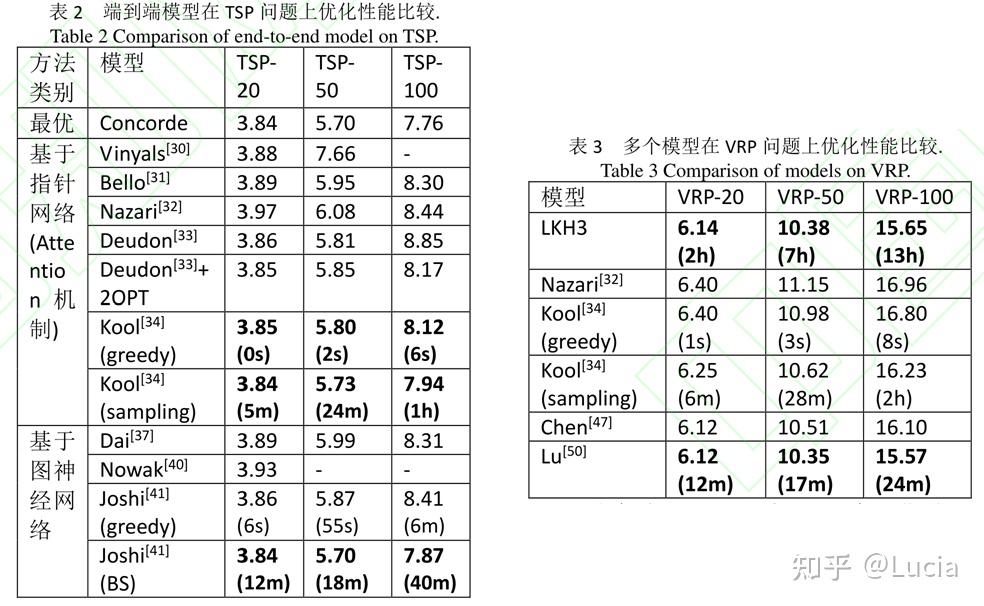
Bello等人采用强化学习方法训练Pointer Network模型，他们将每个问题实例视为一个训练样本，以问题的目标函数作为反馈信号，采用 REINFORCE 强化学习算法进行训练，并引入Critic网络作为baseline以降低训练方差。

进一步地，Nazari 等人将Pointer Network拓展至具有动态特性的VRP问题，作者将输入分为两部分, 包括静态输入(节点位置/坐标)和动态输入(节点需求)，由于考虑到在输入端改变节点的顺序不会影响问题的求解，因此作者将Encoder输入层的LSTM替换成简单的一维卷积层，从而可以有效降低计算成本，并仍然采用REINFORCE强化学习算法进行训练。

Deudon等人借鉴Transformer模型改进了传统的指针网络模型，其Encoder部分采用了与 Transformer模型Encoder部分相同的结构。其Decoder部分将最近三步的决策进行线性映射得到参考向量 , 从而降低模型复杂度 , 其Attention计算方式与传统Pointer Network模型相同，仍然采用REINFORCE方法对该模型进行训练。

Kool等人借鉴Transformer模型，提出了一个可以利用Attention机制求解多种组合优化问题的新方法，该模型的Encoder部分采用了和Transformer模型相同的Multi-head Attention机制，但Decoder部分和Attention机制存在很大不同，首先该模型每一步的解码过程中考虑的是第一步所做的决策和最近两步的决策，采用了Transformer模型的Self-Attention计算方法，增加了更多计算层以提高模型的表现。文章对强化学习训练算法也进行了改进，前述所有文章均采用REINFORCE算法结合Critic-baseline的方式进行训练，而这篇文章设计了一种 rollout baseline来代替Critic神经网络：即在之前训练过程中得到的所有策略模型里，选择在测试集中表现最好的模型作为基线策略，并采用贪婪方式进行动作选择，将利用该基线策略对状态 $s$ 求解得到的目标函数值作为基线 $b(s)$ ，如果当前策略比历史最优策略的表现好，则进行正向激励，从而对当前策略进行评价和参数更新。

Ma等人结合Pointer Network和图神经网络设计了一种图指针网络(Graph Pointer Network, GPN)用来求解大规模TSP问题以及带时间窗约束的TSP问题。该模型的Encoder包含两部分：Point Encoder以及Graph Encoder，Point Encoder对城市坐标进行线性映射, 并输入到 LSTM中得到每个城市的点嵌入，Graph Encoder通过GNN图神经网络对所有城市进行编码, 得到每个城市的图嵌入。模型根据图嵌入和点嵌入，基于Attention 机制计算每一步城市选择的概率，并引入Vector context提高模型的泛化能力。文章采用分层强化学习方法(Hierarchical RL, HRL)对模型进行训练。

Wu等人发现现有的机器学习方法都专注于构造启发式，通过在每个步骤中向部分解添加一个节点来逐步创建一个完整解。尽管这种方法相对较快，但可能产生与最优解具有较大差距的解。所以提出一种直接学习改进启发式求解TSP问题的方法，而不是学习构造启发式。改进启发式算法从初始解开始，通过应用局部算子从邻域得到一个新的解，迭代地替换现有解，以获得更好质量的解。然后提出了一种基于Transofmer中self-attention机制的policy network，并使用Actor-critic算法对policy network进行训练。

B. 图神经网络

图神经网络是近年来提出的能够有效处理图结构数据的新方法，因此部分学者研究如何利用图神经网络对组合优化问题进行建模，其核心思想是根据每个节点的原始信息(如城市坐标)和各个节点之间的关系(如城市之间的距离)，利用图神经网络方法计算得到各个节点的特征向量，根据各个节点的特征向量进行节点预测、边预测等任务。

根据图神经网络计算得到的各个节点的特征向量，可以进行组合优化问题的求解，如针对节点选择问题(如最小顶点覆盖问题)，可以将图神经网络得到的节点特征向量 $h_v^{(t)}$ 以一个全连接层神经网络映射到节点选择概率，从而根据概率进行节点的选择。针对边选择问题(如TSP问题)，可以以两个节点的特征向量作为输入，以一个全连接层神经网络映射得到一个选择概率，即两点之间存在边的概率，从而进行边选择。值得注意的是，按照概率进行边的选择并不一定可以构成一个完整的哈密顿回路，因此需要辅以搜索方法进行解的构造。

监督学习方法

Li等人采用图神经网络对最小顶点覆盖问题、最大独立集问题、极大团、适定性问题进行了研究，由于所研究问题均为点选择问题，与TSP问题不同，对节点选择的顺序无要求，因此文章没有采用逐步添加节点的方式构造解，而是使用GCN图神经网络直接输出所有点选择概率的估计值，并基于该估计值以引导树搜索的方式构造可行解。为了解决问题可能存在多个最优解的情况，文章采用hindsight loss方式输出多个概率分布，在此基础上进行树搜索，并采用局部搜索的方式对解进行再处理。

Mittal等人结合图神经网络、DQN以及贪婪策略进行解的构造，作者采用了图卷积神经网络(Graph Convolutional Networks, GCN)对图结构进行建模。它由两个训练阶段组成：一个有监督的GCN学习有用的单个节点embedding和一个深度神经网络预测共同形成(n个最优或接近最优)解集的节点。也就是，GCN识别潜在的解节点，并将它们传递给深度神经网络，该网络学习用于预测解集的Q函数。

强化学习可以学习有效的启发式方法来解决通常为NP-hard的组合优化问题，Barret等人发现之前的方法都是每次添加一个元素来构建解，然而这种方法的不可逆性阻止了Agent修改其早期的决策，他们认为Agent应该通过在测试时学习探索来不断改进解，进而提出了ECO-DQN模型。

Nowak等人和Joshi等人利用图神经网络对选择各个”边”的概率进行估计，以TSP问题为例，利用图神经网络模型输出一个邻接矩阵， $d_{ij}$ 代表两点之间存在边的概率， $d_{ij}$ 值大则节点 $i$ 和 $j$ 大概率相连。随后根据各个边出现概率的估计值，使用波束搜索(beam search)的方式构造最终的可行解。二者均采用监督方法进行训练，即利用LKH3或Concorde求解器构造大量“坐标-最优路径”的训练数据，根据最优解的真实邻接矩阵和图神经网络输出的邻接矩阵计算交叉熵，以交叉熵为损失函数训练模型。Nowak等人使用的是GNN模型，Joshi等人采用的是GCN模型。

Prates等人求解TSP决策问题(图 $G$ 是否存在一个代价小于预定值的哈密顿路径？)，将GNN用于将每个节点每条边嵌入到多维向量中。该模型作为消息传递算法运行：边迭代地与连接的节点交换信息。在终止时，模型输出是否存在符合期望成本(即，小于预定常数)的路线。

Lemos等人解决了图染色问题的决策版本(图 $G$ 是 $C$ 色可染吗？)。模型基于TSP决策版本中的消息传递思想。节点和边被嵌入到高维向量中，通过与相邻节点的信息交换进行更新。该模型还为每种颜色生成一个全局图嵌入。节点颜色的邻接矩阵将每种颜色与图中的所有节点相关联，因此最初任何节点都可以被分配给任何颜色。在相邻节点之间以及节点和颜色之间的消息迭代结束时，通过节点投票获得最终的二进制答案。

Selsam等人也设计了一种基于消息传递思想的方法，开发了一种新的MPNN，它被训练成一个分类器来预测SAT问题的可满足性。

强化学习方法

Dai等人采用structure2vec图神经网络对当前解的图结构进行建模, 并根据图神经网络计算剩余可选节点中各个节点的Q值，随后基于贪婪策略根据Q值选择一个新的节点添加到当前解中，直至得到完整解。作者采用了深度Q网络(Deep Q-Network, DQN)算法对该图神经网络的参数进行训练，以使模型输出准确的Q值估计。

Abe等人遵循Dai等人提出的体系结构，并用适用于组合优化问题的AlphaGO Zero方法代替Q-Learning。

基于深度强化学习(DRL)的组合优化方法主要分为基于DRL的端到端方法和基于DRL的局部搜索算法，其中端到端方法主要包括基于Pointer Network的端到端方法和基于图神经网络的端到端方法两类 (摘自文章[2])

基于DRL的端到端方法：给定问题实例作为输入，利用训练好的深度神经网络直接输出问题的解，其中神经网络的参数一般利用深度强化学习方法训练得到。具有求解速度快，泛化能力强的优势，但解的最优性很难保证；

基于DRL的局部搜索方法：利用DRL方法改进迭代搜索类方法，对解搜索的启发式规则进行学习和选择。基于深度强化学习改进的局部搜索方法具有较好的优化效果，但其本质上仍然是迭代型搜索算法，求解速度仍然远不及端到端方法。

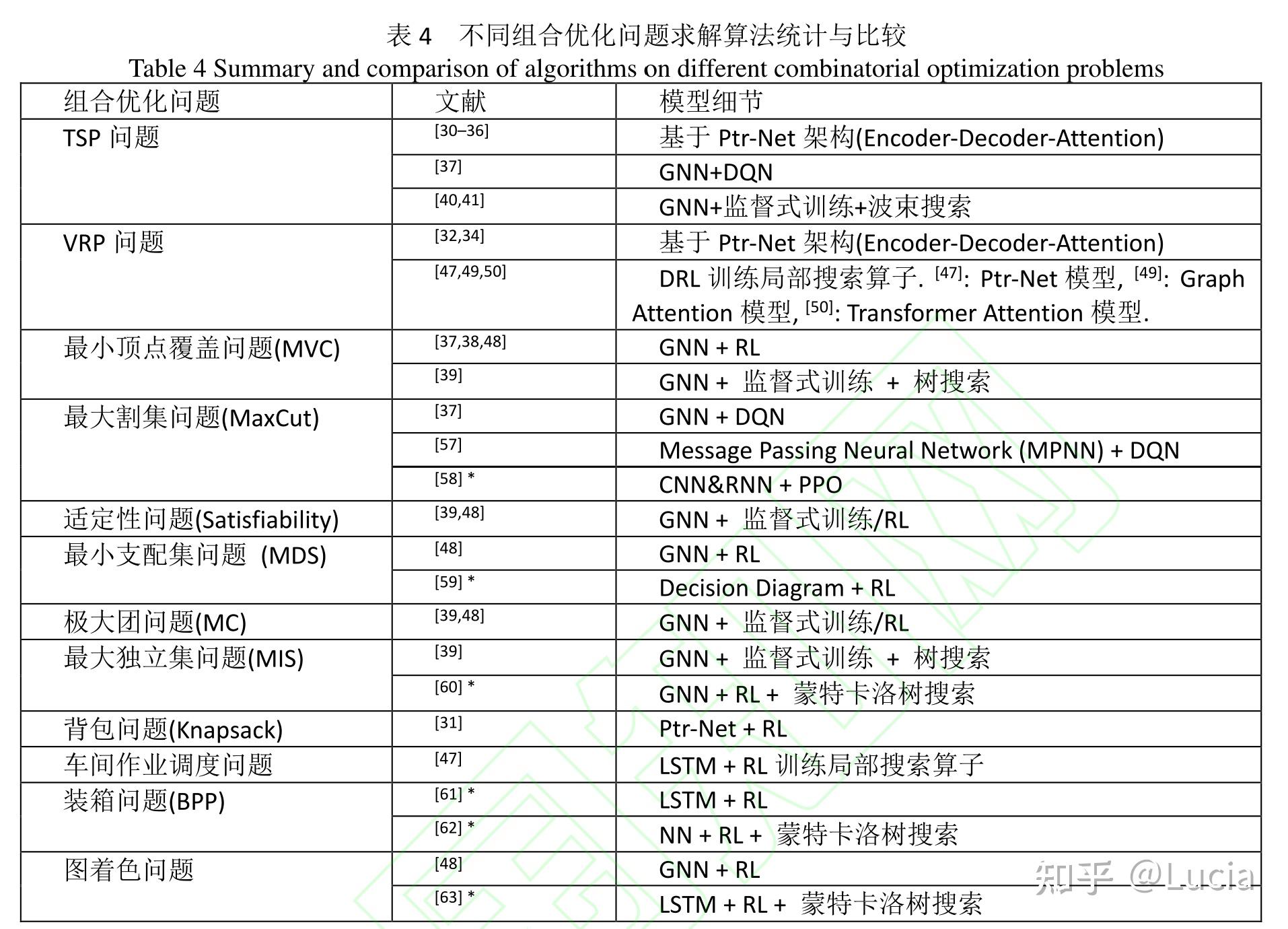
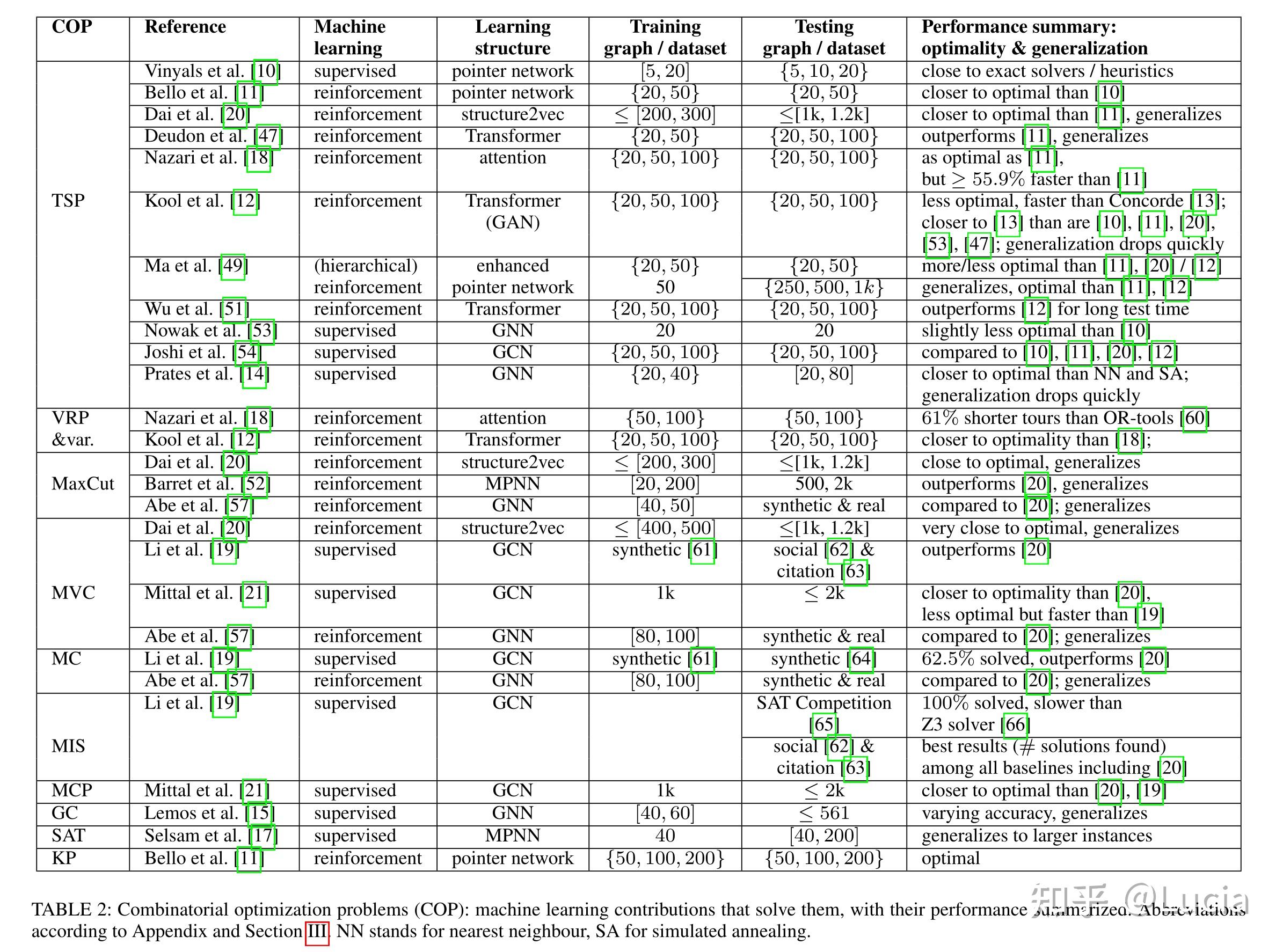
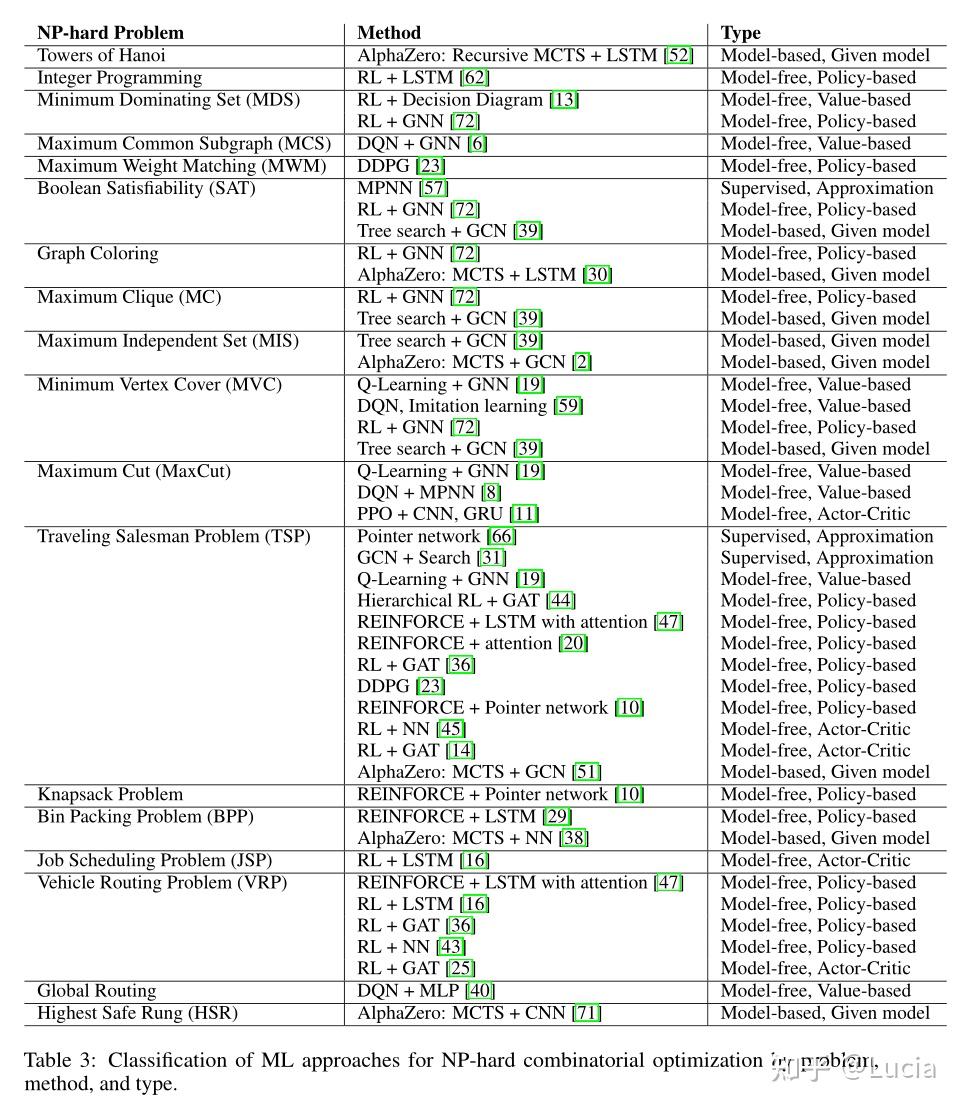
按问题、方法、类型对NP-hard组合优化问题的ML方法进行分类 (摘自文章[3])

求解组合优化问题的机器学习方法可以分为监督学习方法和强化学习方法，强化学习方法可以进一步分为model-free和model-based的方法。model-free方法可以进一步分为value-based方法、policy-based的方法或actor-critic方法，它是前两者的组合。model-based方法可以进一步分为给定模型的方法和学习模型的方法。