上一章传送门：

下个星期课变得好少，我最爱的咸鱼生活开始喽~~~

接上上次的牛顿法，这次开始的两篇文章写写拟牛顿法。

目录：

• 拟牛顿法
• 拟牛顿法框架
• 拟牛顿法是在 下的最速下降法
• 几种经典的拟牛顿算法
• SR1
• DFP
• BFGS
• SR1,DFP,BFGS之间的关系
• Broyden族
• 代码实现三种拟牛顿算法

回顾一下牛顿法的表达式：

上一节说过了牛顿法的缺陷主要在于? 的求取和存储很消耗资源，对于较高维度的数据使用牛顿法求解比较困难。既然 ?的求取和存储很困难，那么我们是否可以近似求得 ?呢？

拟牛顿法(Quasi-Newton methods)的思路就是通过在牛顿法的迭代中加入近似求取每一步Hessian矩阵的迭代步，仅通过迭代点处的梯度信息来求取Hessian矩阵的近似值。现在我们把Hessian矩阵在第 步?的迭代的近似值记作 ?。很显然，我们希望 ?，在原本的牛顿法中，我们有：

那么通过 使用?代替? ，我们的迭代式就变成了：

当然，既然是近似，我们当然不能保证? 能够比较好地近似? 步迭代的Hessian矩阵，所以我们需要通过某种映射来对? 多迭代得到 ?来使得 ?能够比较好地近似第 ?步的Hessian矩阵。除此之外，你会发现，牛顿法需要的Hessian矩阵实际上只是需要使用它的逆矩阵，既然计算Hessian矩阵很烦，计算逆矩阵也很烦，那我们何不直接近似Hessian矩阵的逆矩阵呢？我们记? ，再结合迭代近似值的想法，我们有如下的式子：

fine，其实我们已经得到拟牛顿法了。不同于之前的优化方法，拟牛顿法是一个思想而不是具体的方法，只要迭代形式满足上述迭代式，并且能够收敛，那么这样的方法都是拟牛顿法。那么接下来介绍的每一个具体的拟牛顿法都是在确定 ?怎么确定，怎么更新。

有了之前的认识，我们可以大致写出拟牛顿法的算法过程。

当然，你也可以在更新迭代点时增加步长因子，使其变成阻尼拟牛顿法：

如何根据 ?处的信息更新 ?会在后面讲到，它确定了具体的拟牛顿法。

在具体展开有哪些可以使用的拟牛顿法之前，我觉得我们可以对牛顿法和拟牛顿法来做个比较，来获取一些拟牛顿法本身的性质亦或是难能可贵的认识，这会是在实际工程应用中难以获取的。

我们完全可以从另一个角度来看这个问题，类似于牛顿法的推导过程，我们现在处在迭代点? 处，我们希望在下一步迭代? 后，? 能尽可能地比? 小。为了更好地观察? 和? 之间到底差多少，我们可以使用Taylor展开式：

舍去?的高阶项，我们有：

为了使得? ，此处默认?

也就是说，在误差允许的情况下(?不要太大，Taylor展开式的领域近似，懂的都懂，不懂的我也没有办法=_=)， ?比? 小 ?。因为我们希望? 尽可能比 ?小，自然而然我们希望他们两之间的差值 ?尽可能大。注意到此处的 ?是固定的，也就是我们此时考察的函数在迭代点 ?处的梯度 ?是固定的，所以我们希望动一动 ?，来让 ?尽可能变大。因此，我们的问题变成了如下的优化问题

但是，你会发现，当? 与 ?的夹角固定时，只要我们把? 拉得足够大，那么 ?就会变得无限大，这样的结果是没有意义的。因此我们需要对 ?做一个约束，为了和之前的拟牛顿法的? 联系起来，我们使用椭球范数 ?来约束 ?的取值，我们将?约束为一个定值（? 定义为 ?），不妨就把这个定值设为1吧。那么我们要优化的问题就是如下的式子：

由Cauchy-Schwartz不等式，可得：

当且仅当 ?时，上述不等式等号成立。

故，在我们将 ?在 ?意义下的椭球范数设为定值时，可以得到下降幅度最大的方向为? 。因此我们可以说拟牛顿法是在? 下的最速下降法。

由于每次迭代时的 ?都会变化，那么度量 ?的范数也会随之变化，因此，我们会将这样的方法称为变尺度法

那么当 ?时，拟牛顿方向变为梯度下降方向，所以我们也可以说梯度下降法是在? （ 范数）下的最速下降法；而普通的牛顿法则是在? 下的最速下降法。

还记得在拟牛顿法框架中讲到的模糊不清的最后一步——“根据? 处的信息更新 ?”吗？下面所述便是这个步骤的具体展开。

下面介绍三种具体的拟牛顿法，而推导它们的关键则是确定如何迭代得到每步迭代点Hessian矩阵逆矩阵的倒数? 的近似值 ?。也就是如何确定? 的迭代更新式。

首先做几个符号的规定，来为我们后续的推导做符号运算上的简化。记? 。

很明显，我们就有：

SR1的全称为Symmetric Rank-One，是William C. Davidon在1956年提出的，但由于缺少收敛性分析，所以Davidon的论文被拒稿，导致SR1算法没能成为第一个公认的拟牛顿法。

SR1确定?迭代式的逻辑比较简单——根据? 处的信息得到一个修正量? 来直接加上? 来更新? ，也就是如下的式子：

由于我们希望? ，所以我们有：

由于? 和 ?都是对称矩阵，所以 ?也应该是一个对称矩阵。

而SR1算法就直接把这个对称矩阵? 设为 ?，那么迭代式为：

其中? 。

很显然? 是对称矩阵。至少这个设置上是合理的，那么接下来就根据整个拟牛顿法中的其他条件来把? 和 ?给表示或是整合成其他的表达。

我们在①的两边乘上? ，再根据 ?，我们有：

其中 ?是实数，所以我们有：

为了后续的运算方便，我们把 ?记作? ，也就是：

②式还可以写成? ，我们将③式带入其中可得：

注意到? 和 ?都是实数，所以上式也能写成：

很显然 ?才能使上式成立，因此：

将③和⑤代入①中可得：

因此我们得到了SR1更新?的迭代式：

结合之前的拟牛顿法框架，我们可以整合出SR1算法的具体步骤：

SR1虽然能近似 ?，但是我们无法证明SR1更新得到?的 一定是正定的。也就是说，SR1拟牛顿法确定的拟牛顿方向不一定是下降方向=_=。

DFP是其发现者Davidon, Fletcher, Powell的开头大写字母拼成的，也是第一个公认的拟牛顿法。

其基本思路和SR1差不多，也是想着确定一个对称矩阵修正量? 来更新? ，只不过SR1是令? ，而DFP是给与了 ?更大的自由度。DFP中，我们令 ?，那么? 的迭代更新式为：

其中的 ?和? 都是待定的系数。

那么接下来和推导SR1一样咯，我们在①式的两边右乘上? 可得：

由于我们给与了 ?更多的自由度，因此，仅凭上述的信息，我们当然是无法确定? 的值的。也就说满足上式的?的 取值其实是不唯一的。在DFP中，我们取 。别问为什么，问就是推导方便、结果简单、结果收敛性好说明。

接下来便是确定 ?和 ?的过程了。很显然，这两个量的取值也不唯一。对于②式，我们可以改写为：

为了好算且方便，我们干脆直接令 ?。

对于 ?，由于我们之前取了? ，所以

为了使得上式恒成立，我们有 ?，因此，我们有? 。

同理我们也可以得到 ?，因此，我们有 ?。

将 ?的取值代入①式中，我们就可以得到DFP更新? 的迭代式了：

DFP的推导过程看似随意，但是DFP的迭代公式也可以通过如下的优化问题的解得到：

其中 且 满足拟牛顿方程。此处不做推导，无聊的同学请自行推导。

结合之前的拟牛顿法框架，我们可以整合出DFP算法的具体步骤（水行数警告）：

BFGS这个算法的记忆没有诀窍=_=，因为它是下面这四个人分别提出的，所以和DFP一样，用四个人的名字的开头字母命名。

其推导其实和DFP一样，不过BFGS是从 ?出发来推导的。（还记得 ?是啥吗？? 是我们对 ?的近似）

对于? ，我们采用和DFP一样的思路，也就是考虑 ?的rank-tow修正：

后面和DFP一模一样，我们可以得到 ?的迭代公式：

你会发现，我们其实就是把DFP中的? 与 ?互换位置，把 ?换成 ?罢了。

那么我们要求的? 不就是 ?吗？那么我们直接对①式两边取逆就行了。你会发现右式的取逆你算不出来，这时你就需要SMW公式了：

我们可以递归地使用上面的式子，令 ?代入SMW公式中。其中? 的计算再用一次SMW公式，反正通过一通暴算，最终我们得到：

如此，我们便得到了BFGS 的?迭代更新式：

于是，我们得到了BFGS拟牛顿法的具体步骤(我真不是在水行数~~~)：

有了之前的SMW公式，我们可以尝试求取上述的三个拟牛顿法的? 的更新公式，毕竟 ?才是对Hessian矩阵的近似，我们需要知道每步对Hessian矩阵的近似情况，这个对收敛性分析会有比较大的帮助。

SR1的迭代式为

两边取逆，使用SMW公式，可以得到SR1中，? 的迭代式

可以发现，结果就是将? 和 ?交换，把? 和 ?交换。

因此，我们说SR1是自对偶的。

再看看DFP和BFGS迭代公式两边取逆后的结果：

可以看到DFP和BFGS公式高度对称，只需? 就可以在DFP和BFGS公式之间相互转换。

因此，我们说DFP和BFGS互为对偶。

既然DFP和BFGS是互为对偶的，那用哪一个比较好呢？你当然可以通过若干组实验来测试哪个的性能的更优，或者对其收敛一通验证。但是一个比较的朴素的做法就是“我都要”，也就是取DFP迭代式和BFGS迭代式的正加权组合：

其中 。?我们记? ，然后将 ?和 ?的表达式代入其中可得：

随着 ?遍历? 内的值，我们可以得到一系列的 ?。我们将这一系列的? 的集合称为Broyden族。

而且根据定义， ?时，? 即为BFGS校正；? 时，? 即为DFP校正。而且可以证明，DFP和BFGS校正都是保持正定的，且我们的? ，所以我们只要满足 ?就可以保证Broyden族校正都是保持正定的。

终于到了我最爱的编程环节了，这次我们就不像上次的梯度下降法一样造轮子了，我们直接调取写好的优化库来快速完成项目需求。

因为笔者是个Python小白，所以关于数值优化的Python第三方库我知道如下三个：cvxpy,cvxopt,scipy。其中scipy.optimize子库有关于优化的算子。

由于上述的三个库都是基于numpy库开发的，所以在调用pip指令安装时，请先安装numpy库

我翻了一上午的源代码和document，并没有在cvxpy和cvxopt中找到关于拟牛顿法的算子。因此，笔者下面采用scipy.optimize来实现三种拟牛顿法。如果你没有安装相关的依赖库，请打开命令行，输入以下命令来自动安装（请确保你的Python解释器的Script文件夹的路径已被添加到环境变量Path中）：

pip install numpy, matplotlib, scipy -i https://pypi.tuna.tsinghua.edu.cn/simple

此处我们分别使用SR1，DFP和BFGS拟牛顿法优化如下的函数：

其中 ?， ， ?代表向量 ?的第? 个维度上的元素。

已知上述的优化问题的最优点为 ?，取迭代初值为 ?。

我们首先先实现上述的函数，我通过一个函数获取一个映射? ：

下面所有的代码都写在一个文件中

# -*- utf-8 -*-
# date: 2020-10-22
# author: 锦恢
?
from scipy.optimize import fmin_powell, fmin_bfgs, fmin_cg, minimize, SR1
import numpy as np
import matplotlib.pyplot as plt
?
def r(i, x):
    if i % 2 == 1:
        return 10 * (x[i] - x[i - 1] ** 2)  # 因为ndarray数组的index是从0开始的， i多减一个
    else:
        return 1 - x[i - 2]
?
def f(m):
    def result(x):
        return sum([r(i, x) ** 2 for i in range(1, m + 1)])
    return result

通过 ?我们就可以获取上述需要优化的函数的映射。

为了观察拟牛顿法运行过程中迭代点的下降情况，我们需要计算

# 获取retall的每个点的值损失|f(x) - f(x^*)|
def getLosses(retall, target_point, func):
    """
    :param retall: 存储迭代过程中每个迭代点的列表，列表的每个元素时一个ndarray对象
    :param target_point: 最优点，是ndarray对象
    :param func: 优化函数的映射f
    :return: 返回一个列表，代表retall中每个点到最优点的欧氏距离
    """
    losses = []
    for point in retall:
        losses.append(np.abs(func(target_point) - func(point)))
    return losses

scipy.optimize子库中的许多执行拟牛顿法的算子提供了call_back参数，该参数要求传入一个函数对象，在拟牛顿每步迭代完后，传入的call_back函数会被调用。由于使用SR1法的算子minimize无法返回迭代过程中的每一个迭代点（也就是retall），于是我们需要call_back函数来将迭代完的点传入外部的列表，从而获取SR1的retall。除此之外，我们可以使用call_back函数来指定迭代停止的条件。

我们编写一个返回函数对象的函数，它会根据我们传入参数的不同返回不同的call_back函数：

sr1_losses = [] # 存储SR1的retall的列表
func = f(4) # 获取需要优化的函数
?
# 通过callback方法来添加迭代的停止条件
def getCallback(func, target_point, ftol, retall):
    """
    :param func: 优化目标的函数
    :param target_point:  目标收敛点
    :param ftol: 收敛条件：|f(x) - f(x^*)| < ftol时，迭代停止
    :param retall: 是否存储迭代信息
    :param extern_retall: 如果retall为True， 填入一个列表，迭代信息会存在这个列表中
    :return: call_back函数对象
    """
    def result(xk, state=None):
        if retall:
            global func, sr1_losses
        loss = np.abs(func(target_point) - func(xk))
        if loss < ftol:
            return True
        else:
            if retall:
                sr1_losses.append(loss)
            return False
    return result

为了方便可视化，我们将数据可视化的逻辑封装到一个函数中：

# 绘制下降曲线
def plotDownCurve(dpi, losses, labels, xlabel=None, ylabel=None, title=None, grid=True):
    plt.figure(dpi=dpi)
    for loss, label in zip(losses, labels):
        plt.plot(loss, label=label)
    plt.xlabel(xlabel, fontsize=12)
    plt.ylabel(ylabel, fontsize=12)
    plt.title(title, fontsize=18)
    plt.yscale("log")
    plt.grid(grid)
    plt.legend()

接着我们定义一下迭代初值、最优点和终止条件的阈值 ?（? 时，迭代停止）并获取三个拟牛顿法需要的call_back函数。

x_0 = np.array([1.2,1.0,1.0,1.0])   # 迭代初值
target_point = np.array([1,1,1,1], dtype="float32")     # 最优点
FTOL = 1e-8     # 终止阈值
?
sr1_callback = getCallback(func, target_point, ftol=FTOL, retall=True)
dfp_callback = getCallback(func, target_point, ftol=FTOL, retall=False)
bfgs_callback = getCallback(func, target_point, ftol=FTOL, retall=False)

下面我们我们使用minimum,fmin_powell,fmin_bfgs来实现三种拟牛顿法的迭代，并把DFP和BFGS的retall存入列表中。

minimum = minimize(fun=f(4), x0=x_0,        # 通过minimize函数执行SR1，根据内嵌的callback填充loss，并返回OptimizerResult对象
                   method="trust-constr",
                   hess=SR1(),
                   callback=sr1_callback)
?
dfp_minimum, dfp_retall = fmin_powell(func=func, x0=x_0,
                                      retall=True,
                                      disp=False,
                                      callback=dfp_callback)
dfp_losses = getLosses(dfp_retall, target_point, func=func)
?
bfgs_minimum, bfgs_retall = fmin_bfgs(f=func, x0=x_0,
                                      retall=True,
                                      disp=False,
                                      callback=bfgs_callback)
bfgs_losses = getLosses(bfgs_retall, target_point, func=func)

迭代做完后，我们自然想知道结果如何，可视化是一个直观的方法，我们将plt画布的分辨率调为150，设置一下各个轴的名称，将它可视化出来：

plotDownCurve(dpi=150,  
              losses=[sr1_losses, dfp_losses, bfgs_losses],
              labels=["SR1", "DFP", "BFGS"],
              xlabel="#iter",   
              ylabel="value of $|f(x) - f(x^*)|$",
              title="losses curve of SR1, DFP and BFGS")
plt.show()  

out:

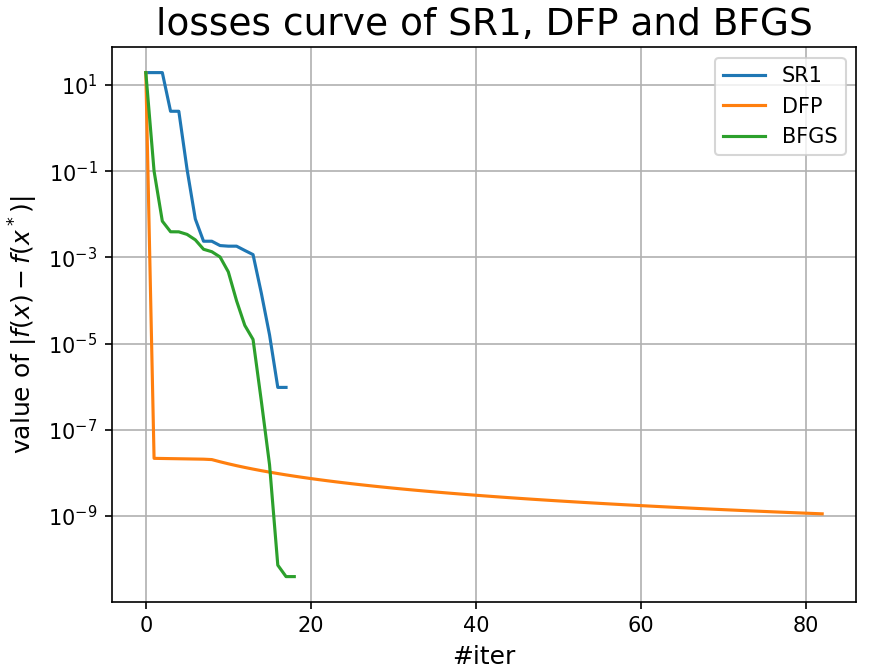
我们可以查看三种方法得到的最优点和它们具体的迭代次数：

print(f"SR1\	最终迭代点:{minimum.x.tolist()}, 共经历{minimum.cg_niter}次迭代")
print(f"DFP\	最终迭代点:{dfp_minimum}, 共经历{len(dfp_losses)}次迭代")
print(f"BFGS\	最终迭代点:{bfgs_minimum}, 共经历{len(bfgs_losses)}次迭代")

out:

SR1 最终迭代点:[0.9999962062462336, 0.9999929560009194, 0.9999943517470878, 0.9999915182271095], 共经历35次迭代
DFP 最终迭代点:[0.99998036 0.99996341 1.         1.        ], 共经历83次迭代
BFGS    最终迭代点:[0.99999547 0.9999909  0.99999572 0.99999144], 共经历19次迭代

可以看到三种方法都成功收敛到了 ?，说明程序是没问题滴~~~

下一章传送门：