本期我们介绍算术优化算法(The Arithmetic Optimization Algorithm ,AOA)。该算法由Laith Abualigah等人(又有Mirjalili教授哦)于2021年提出,主要利用了数学中加减乘除这四种运算符的定义以进行模型优化,具有较好的应用前景。
算术是数论的一个基本组成部分,与几何、代数和分析一样,它也是现代数学的重要组成部分之一。大家都知道,算数中最常见的运算符就是“加(A)减(S)乘(M)除(D)”,因此在算法中使用这些简单的算子作为数学优化,从一组候选方案(解决方案)中确定符合特定标准的最佳元素。对于算法中探索与开发的关系,作者利用这四个运算法给出了答案:
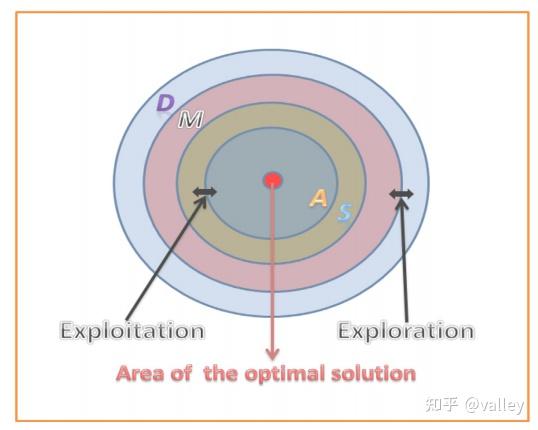
初始化阶段
初始化种群后,算法内设置了一个加速系数(Math Optimizer Accelerated,MOA)来控制算法的搜索阶段:
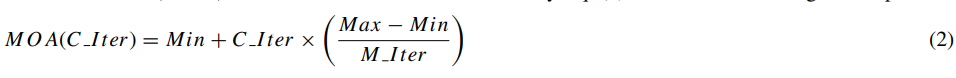
其中C_Iter、M_Iter分别为当前迭代次数、最大迭代次数,Min、Max分别为加速函数的相对最小、最大值。
MOP_Max=1;
MOP_Min=0.2;
MOA=MOP_Min+C_Iter*((MOP_Max-MOP_Min)/M_Iter); %Accelerated function勘探阶段(r1>MOA,r1为[0,1]内一随机数)
根据算术运算符,使用除法(D)或乘法(M)进行的数学计算得到了高分布值或决策,这适合应用至勘探搜索机制。然而,与其他算子不同,D、M由于其高度分散而不能轻易接近目标。图2显示了四种算术运算符在数学计算中的影响和行为:
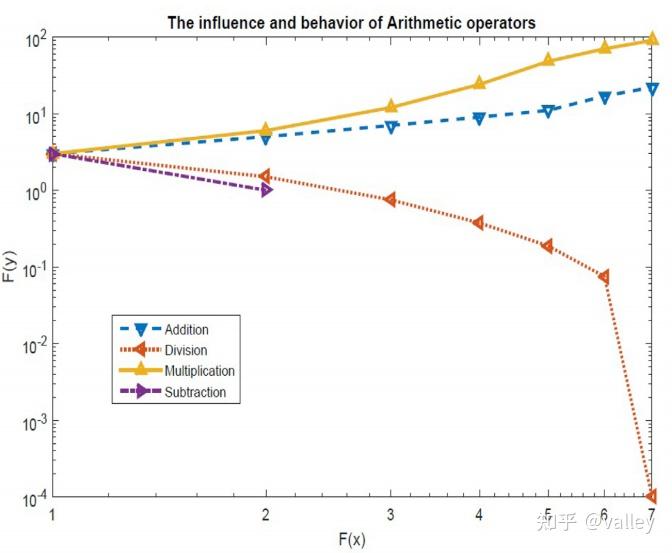
此阶段,算法利用探索算子在搜索区域上进行全局搜索,并基于两种主要搜索策略(除法搜索策略(D)和乘法搜索策略(M))寻找更好的解决方案:
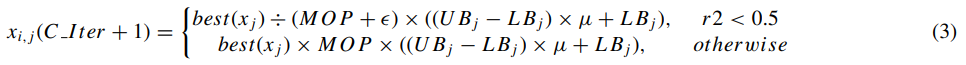
式中,?=2.2204e-16,为随机比例系数,用以产生更多的多样化过程并探索搜索空间的不同区域。r2为[0,1]内一随机数,best(xj )为最优个体xj 在第j 维上的位置,UBj、LBj分别为第j 维上的搜索上、下限。μ是调整搜索过程的控制参数,通常取值为0.5。与MOA类似,算法中设置了一个概率系数(Math Optimizer probability,MOP):

α是一个敏感参数,定义了迭代过程中的开发精度,根据原文的实验,该精度固定为5。
开发阶段(r1≤MOA)
根据算术运算符,使用减法或加法进行的数学计算能够得到高密度的结果,因此非常适合用于开发阶段。在算法中,利用算子(减法和加法)在几个密集区域上深入探索,并基于两种主要搜索策略(即减法搜索策略(S)和加法搜索策略(A))寻找更好的解决方案:
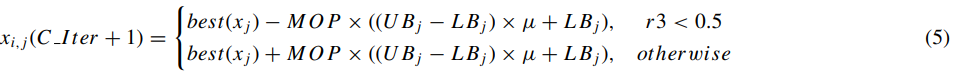
r3为[0,1]内一随机值。该阶段与前一阶段很相似,不过更有助于探索搜索区域找到最优解并保持候选解的多样性。图3显示了所使用的各种运算符如何帮助算法收敛到最佳区域:
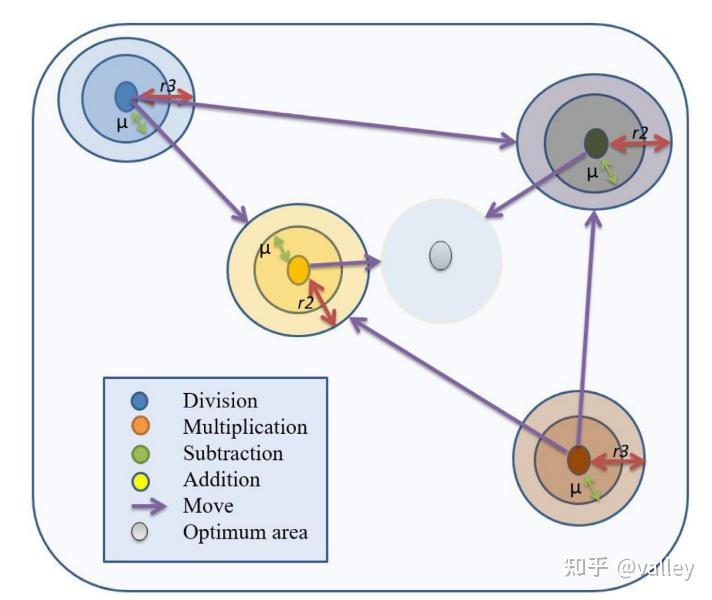
基于此,算法迭代伪代码为:

本次依旧选取PSO算法与AOA算法在标准测试函数上进行对比测试,种群规模设为30,最大迭代次数为500:
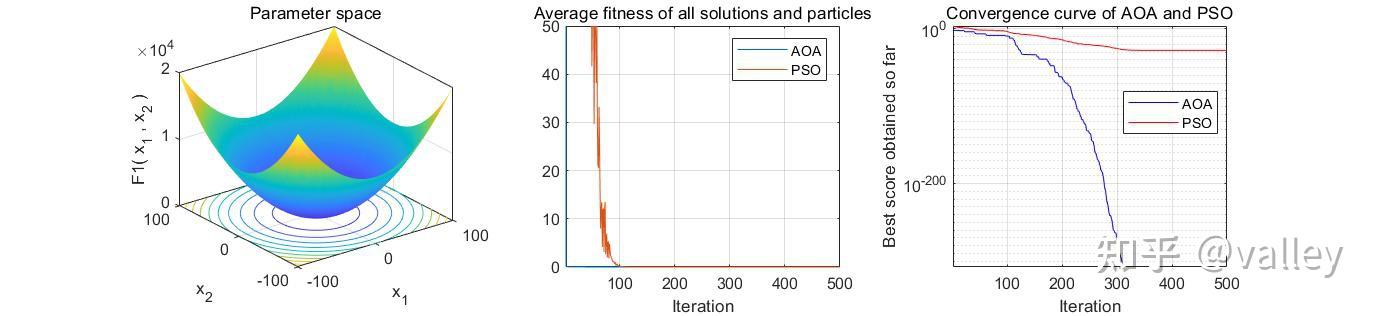
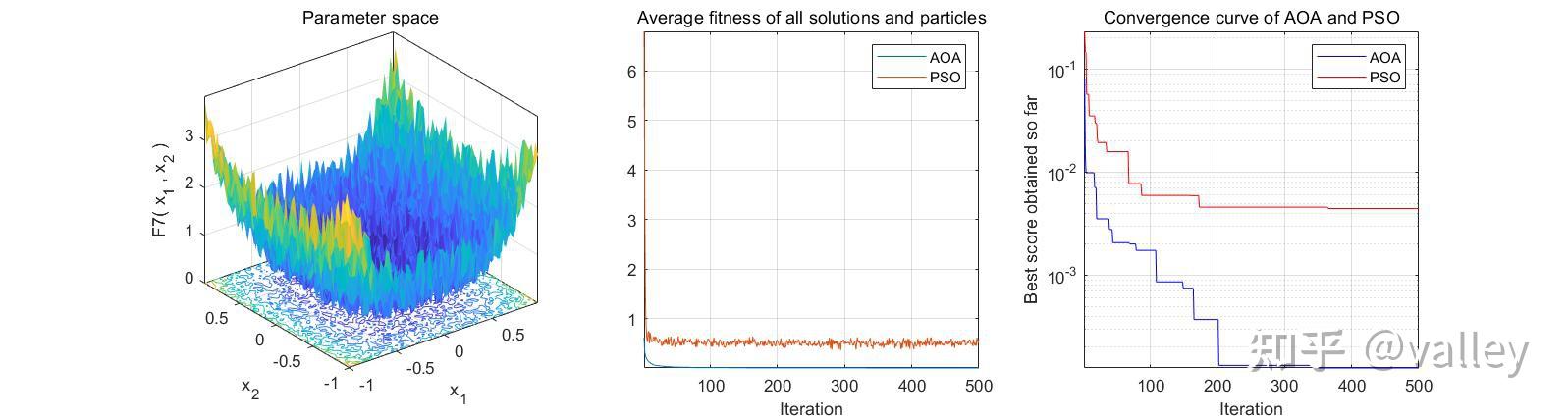
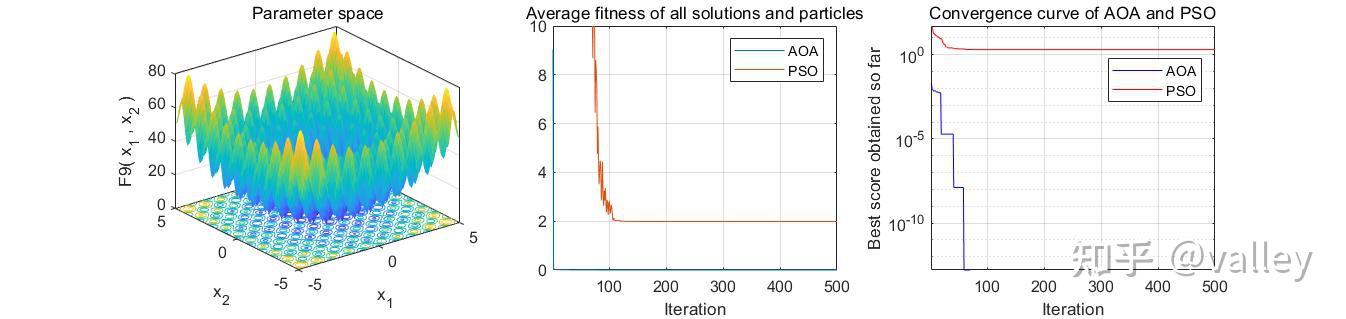
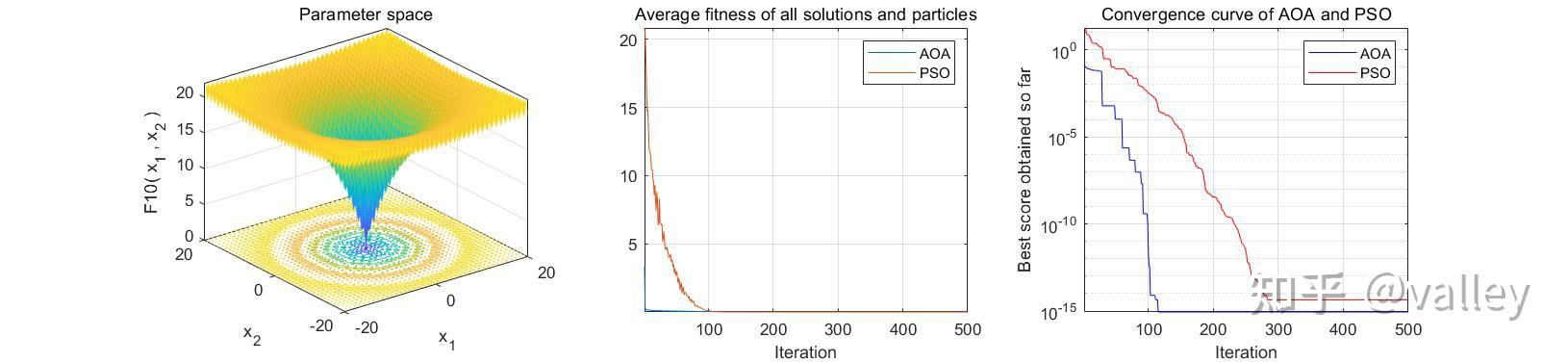
就迭代图像来说,AOA算法性能还是可以的,不过跳出局部最优值的能力仍有待提升。
就算法思路而言,我认为AOA算法与哈里斯鹰优化算法有点相似:设置层层的判断以引导算法利用多种模式进行个体位置更新:
valley:第五弹——哈里斯鹰优化算法这样在避免了单一模式的局限性,也在冥冥之中提高了种群多样性。不过如何把不同的模式做出各自的特点(避免两两相似性过高)是一个难点,而AOA算法中根据加减乘除四种运算法则来定义相应的位置更新方式确实是独具新意~




