本系列文章是阅读雷明老师《机器学习的数学》一书后整理的读书笔记。

首先介绍最优化方法中的相关知识点，下面两幅图是对最优化方法的分类和知识体系的一个总结。

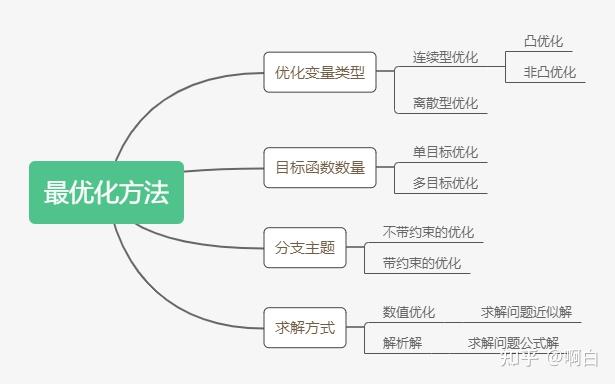
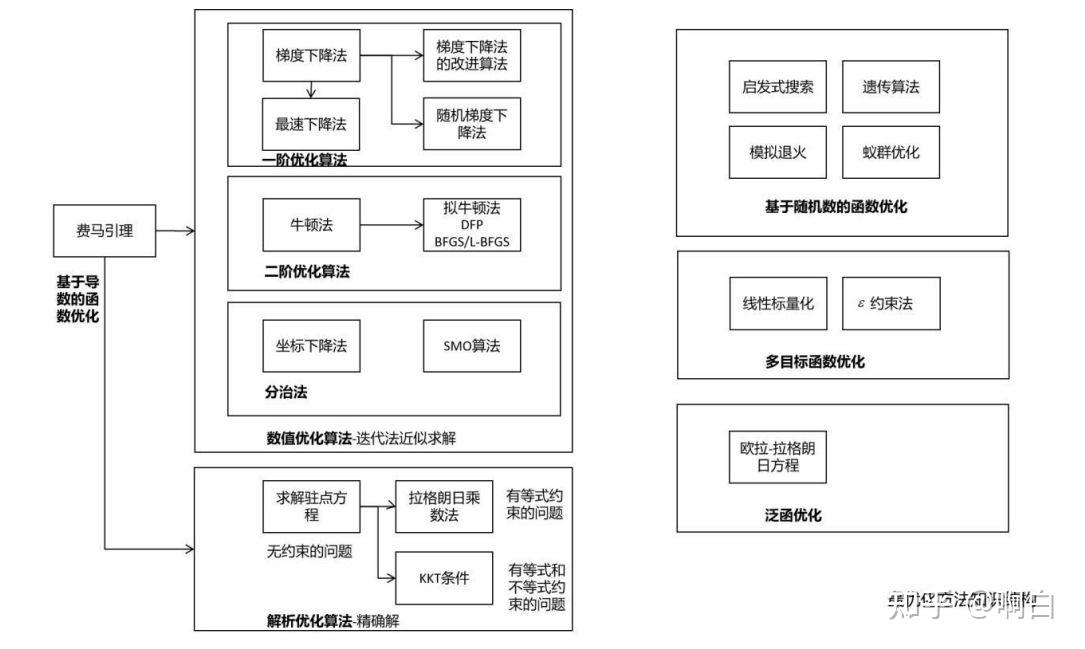
一般将最优化问题统一表述为极小值问题，对于极大值问题，只需要将目标函数反号。其形式定义如下：

其中为优化变量，为目标函数，为优化变量允许的取值集合，称为可行域，它由目标函数的定义域、等式及不等式约束共同确定。可行域之内的解释为可行解。

假设 是一个可行解，如果对可行域内所有点 都有 ，则称 为全局极小值。

对于可行解 ，如果存在其 邻域，使得该邻域内所有满足 的点 都有 ，则称 为局部最小值。

最优化算法的目标是寻找目标函数的全局极值点而非局部极值点。

一阶优化算法是利用目标函数的一阶导数构造 的迭代公式。

梯度下降法（Gradient Descent Method）由数学家柯西提出，它沿着当前点 处梯度相反的方向进行迭代，得到 ，直到收敛到梯度为0的点。其理论依据：在梯度不为0的任意点处，梯度正方向是函数值上升的方向，梯度反方向是函数值下降的方向。

• 证明：梯度反方向是函数值下降的方向

将函数在 点处做一阶泰勒展开：

对上式变形：

如果令 ，则有：

如果 足够小，则可以忽略高阶无穷小项，有：

如果在 点处梯度不为0，则能保证移动到 时函数值增大。相反地，如果令，则有：

则函数值减小。事实上，只要确保

则有

因此，选择合适的增量 就能保证函数值下降，负梯度方向只是一个特例。那么，当增量的模一定时，为什么负梯度方向函数值下降最快呢？

• 证明：增量模一定时，沿着负梯度方向，函数值下降最快

由于

其中 为 和 之间的夹角。因此如果 ，则 ，函数值增大；如果 ，则 ，函数值下降。 沿着负梯度方向即 是特例，如果向量 的模大小一定，则 ， 则在梯度相反的方向函数值下降最快，此时 。

梯度下降法每次迭代的增量为

其中 称为步长或学习率，其作用是保证 在 的邻域内，从而可以忽略泰勒公式中的 项，否则不能保证每次迭代时函数值下降。

由此得到梯度下降法的迭代公式，从起始点 开始，反复使用如下迭代公式

梯度下降法在每次迭代时只需要计算函数当前点处的梯度值，具有计算量小、实现简单的优点。只要未达到驻点处且学习率设置恰当，每次迭代时均能保证函数值下降。

最速下降法是对梯度下降法的改进，它用算法自动确定步长值。最速下降法同样沿着梯度相反的方向进行迭代，每次需要计算最佳步长 。

最速下降法的搜索方向与梯度下降法相同，也就是负梯度方向

在该方向上寻找使得函数值最小的步长，通过求解如下一元函数优化问题实现

通过直接求该函数的驻点实现，这种方法也称为直线搜索，沿着某一确定的方向在直线上寻找最优步长。

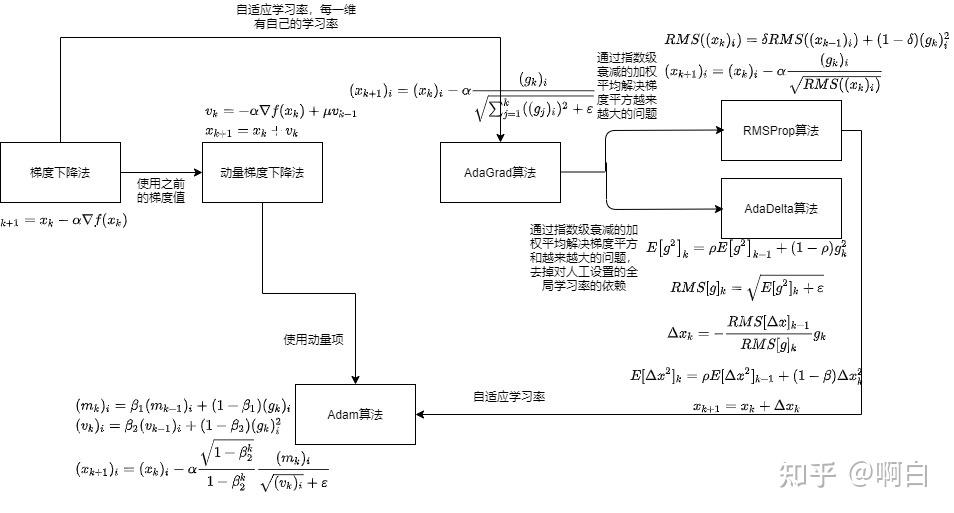
在机器学习中，目标函数通常定义在一个训练样本集上。假设训练样本集有个样本，机器学习模型在训练时优化的目标是这个数据集上的平均损失函数

其中是对单个训练样本的损失函数，是机器学习模型需要学习的参数，是优化变量。

但是如果训练样本每次都用所有的样本，那么计算成本太高了。

• 改进：小批量随机梯度下降法

在每次迭代时只使用个样本来近似计算损失函数。

随机梯度下降法在数学期望的意义下收敛，随机采样产生梯度的期望值是真实的梯度。一种特殊情况是，每次迭代只使用一个训练样本。

除了具有实现效率高的优点之外，随机梯度下降法还会影响收敛的效果。对于深度神经网络，随机梯度下降法比批量梯度下降法更容易收敛到一个好的极值点。