深度学习优化器总结_耀世娱乐-耀世注册登录官方入口

Background

深度学习可以归结为一个优化问题，最小化目标函数 $J(\ heta)$ ；最优化的求解过程，首先求解目标函数的梯度 $\ abla J(\ heta)$ ，然后将参数 $\ heta$ 向负梯度方向更新， $\ heta_{t}=\ heta_{t-1}-\\eta\ abla J(\ heta)$ , $\\eta$ 为学习率，表明梯度更新的步伐大小。最优化的过程依赖的算法称为优化器，可以看出深度学习优化器的两个核心是梯度与学习率，前者决定参数更新的方向后者决定参数更新程度。深度学习优化器之所以采用梯度是因为，对于高维的函数其更高阶导的计算复杂度大，应用到深度学习的优化中不实际。

　　深度学习的优化器有许多种类，学术界的研究也一直十分活跃，个人理解优化器可以分为两个大类。第一类是优化过程中，学习率 $\\eta$ 不受梯度 $\ abla J(\ heta)$ 影响，全程不变或者按照一定的learning schedule随时间变化，这类包括最常见的SGD(随机梯度下降法)，带Momentum的SGD，带Nesterov的SGD，这一类可以叫作SGD系列；另一类是优化过程中，学习率随着梯度 $\ abla J(\ heta)$ 自适应的改变，并尽可能去消除给定的全局学习率的影响，这一类优化器有很多，常见的包括Adagrad Adadelta RMSprop Adam；还有AdaMax Nadam Adamax NadamAMSgrad(ICLR 2018 best paper)，以及最近比较火的Adabound，这一系列可以称为自适应学习率系列。

1.SGD系列

(1)SGD(Stochastic gradient descent)

更新公式： $\ heta=\ heta - \\eta \\cdot \ abla_\ heta J( \ heta)$

SGD的梯度下降过程，类似于一个小球从山坡上滚下，它的前进方向只于当前山坡的最大倾斜方向一致(最大负梯度方向)，每一个时刻的初速度为０

(2)SGDM Momentum 动量

更新公式：

$\\begin{align}\\begin{split}v_t &=\\gamma v_{t-1}+ \\eta \ abla_\ heta J( \ heta) \\\\ \ heta &=\ heta - v_t \\end{split}\\end{align}$

SGD的梯度下降过程，类似于一个小球从山坡上滚下，它的前进方向由当前山坡的最大倾斜方向与之前的下降方向共同决定，小球具有初速度(动量)，不只被梯度制约。SGDＭ克服了之前SGD易震荡的缺点，对比效果如下图：

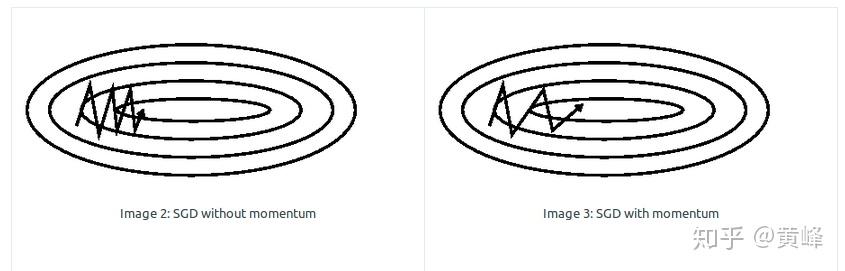
(3)Nesterov accelerated gradient

更新公式：

$\\begin{align}\\begin{split}v_t &=\\gamma v_{t-1}+ \\eta \ abla_\ heta J( \ heta - \\gamma v_{t-1}) \\\\ \ heta &=\ heta - v_t \\end{split}\\end{align}$

和带动量SGD十分接近，带Nesterov的小球，先按上一时刻初速度移动一个小位置，然后在新的位置它的前进方向由当前山坡的最大倾斜方向与之前的下降方向共同决定，见下图

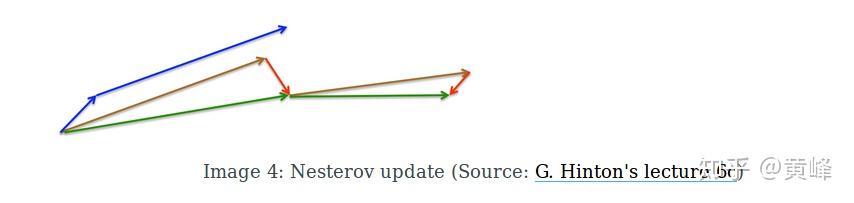
带Momentum的SGD，梯度下降方向由短蓝线(梯度更新 $-\\eta \ abla_\ heta J( \ heta)$ ) 长蓝线(上一时刻动量 $\\gamma v_{t-1}$ )共同决定；带Nesterov的SGD，先在上一时刻动量方向跳跃一下(棕色线)更新位置( $\ heta - v_t$ ),再在新的位置由当前梯度与动量决定下降方向 $\\gamma v_{t-1}+ \\eta \ abla_\ heta J( \ heta - \\gamma v_{t-1})$ .

带Nesterov的SGD,nesterov项在梯度更新时做一个校正，避免前进太快，同时提高灵敏度。

2.自适应学习系列－常见系列

(1)Adagrad

　　通过以往的梯度自适应更新学习率，不同的参数 $\ heta_{i}$ 具有不同的学习率。Adagrad 对常出现的特征进行小幅度更新，不常出现的特征进行大幅度的更新，对比SGD对所有特征进行同样幅度的更新，十分适合处理稀疏数据。

具体的，SGD对每个参数 $\ heta_{i}$ 在每步 $t$ 的更新公式为：

$\ heta_{t+1, i}=\ heta_{t, i}- \\eta \\cdot g_{t, i}$ ；

　　Adagrad对每个参数 $\ heta_{i}$ 在每步 $t$ 的更新公式为：

$\ heta_{t+1, i}=\ heta_{t, i}- \\dfrac{\\eta}{\\sqrt{G_{t, ii}+ \\epsilon}}\\cdot g_{t, i}$ ， $G_{t}\\in \\mathbb{R}^{d \ imes d}$ 是一个对角矩阵，它的每个元素是到步 $t$ 的梯度平方和， $G_{t,ii}=G_{t-1,ii}+g_{t,i}^{2}$ 。

　　Adagrad的参数更新写成向量形式， $\\epsilon$ 是平滑系数，防止零除。

$\ heta_{t+1}=\ heta_{t}- \\dfrac{\\eta}{\\sqrt{G_{t}+ \\epsilon}}\\odot g_{t}$ 。

　　可以看出，随着参数更新， $G_{t,ii}$ 逐渐增大， $\ heta_{t, i}$ 对应的学习率减少最终趋于0。

(2)Adadelta

　　Adadelta是对Adagrad的一个改进，它解决了Adagrad优化过程中学习率 $\\eta$ 单调减少问题。Adadelta不再对过去的梯度平方进行累加，而是改用指数平均的方法计算G_{t}，Adagrad中的 $G_{t}$ 替换为 $E[g^2]_t$ ，

$E[g^2]_t=\\gamma E[g^2]_{t-1}+ (1 - \\gamma) g^2_t＝(1-\\gamma)\\Sigma_{i=0}^{t}\\gamma^{i}g_{t}^{2}$

$\\Delta \ heta_t=- \\dfrac{\\eta}{\\sqrt{E[g^2]_t + \\epsilon}}g_{t}=- \\dfrac{\\eta}{RMS[g]_{t}}g_t$ , $RMS[g]_{t}$ 对应 $g_{t}$ 的均方误差根。

　　此时的Adadelta仍然依赖于全局的学习率 $\\eta$ ，为消除全局学习率的影响，定义新的指数平均方法，

$E[\\Delta \ heta^2]_t=\\gamma E[\\Delta \ heta^2]_{t-1}+ (1 - \\gamma) \\Delta \ heta^2_t$

$RMS[\\Delta \ heta]_{t}=\\sqrt{E[\\Delta \ heta^2]_t + \\epsilon}$

最终Adadelta更新规则为，

$\\begin{align}\\begin{split}\\Delta \ heta_t &=- \\dfrac{RMS[\\Delta \ heta]_{t-1}}{RMS[g]_{t}}g_{t}\\\\ \ heta_{t+1}&=\ heta_t + \\Delta \ heta_t \\end{split}\\end{align}$

(3)RMSprop

RMSprop等价于Adadelta的第一种形式，通常 $\\gamma$ 设为0.9, $\\eta$ 设为0.001

$E[g^2]_t=\\gamma E[g^2]_{t-1}+ (1 - \\gamma) g^2_t＝(1-\\gamma)\\Sigma_{i=0}^{t}\\gamma^{i}g_{t}^{2}$

$\\Delta \ heta_t=- \\dfrac{\\eta}{\\sqrt{E[g^2]_t + \\epsilon}}g_{t}=- \\dfrac{\\eta}{RMS[g]_{t}}g_t$

(4)Adam

在SGDM的基础上，引入自适应学习率

$\\begin{align}\\begin{split}m_t &=\\beta_1 m_{t-1}+ (1 - \\beta_1) g_t \\\\ v_t &=\\beta_2 v_{t-1}+ (1 - \\beta_2) g_t^2 \\end{split}\\end{align}$

$m_{t},v_{t}$ 对应梯度 $g_{t}$ 的一阶二阶矩估计，是有偏估计，校正为无偏估计：

$\\begin{align}\\begin{split}\\hat{m}_t &=\\dfrac{m_t}{1 - \\beta^t_1}\\\\ \\hat{v}_t &=\\dfrac{v_t}{1 - \\beta^t_2}\\end{split}\\end{align}$

Adam 更新规则:

$\ heta_{t+1}=\ heta_{t}- \\dfrac{\\eta}{\\sqrt{\\hat{v}_t}+ \\epsilon}\\hat{m}_t$

上述优化器算法都是很常见了的，

贴一个SGD SGDM Adgrad RMSprop Adam总结图：SGD SGDM Adgrad RMSprop Adam等优化器算法可以归结为一个在线凸优化问题[2],优化算法为：

不同的优化器对应不同的 $\\psi(g_{1}...g_{t}) , \\phi(g_{1}...g_{t})$ 函数，

(3)自适应学习系列－未名系列：AdaMax Nadam Adamax Nadam　AMSgrad(ICLR 2018 best paper)，以及最近比较火的Adabound

AdaMax

　　Adam变体，Adam中用 $l_{2}$ norm度量梯度大小，

$v_t=\\beta_2 v_{t-1}+ (1 - \\beta_2) |g_t|^2$

　　进一步推广为 $l_{p}$ norm形式，

$v_t=\\beta_2^p v_{t-1}+ (1 - \\beta_2^p) |g_t|^p$ ，

　　Adamax便是用无穷范数 $l_{\\infty}$ 度量梯度大小，用于收敛到更稳定的状态

$\\begin{align}\\begin{split}u_t &=\\beta_2^\\infty v_{t-1}+ (1 - \\beta_2^\\infty) |g_t|^\\infty\\\\ &=\\max(\\beta_2 \\cdot v_{t-1}, |g_t|) \\end{split}\\end{align}$

AdaMax update rule: $\\sqrt{\\hat{v}_t}+ \\epsilon$ 被 $u_t$ 代替，

$\ heta_{t+1}=\ heta_{t}- \\dfrac{\\eta}{u_t}\\hat{m}_t$

好的默认设置: $\\eta=0.002, \\beta_1=0.9, \\beta_2=0.999$

Nadam(Nesterov-accelerated Adaptive Moment Estimation)

RMSprop与momentum的组合，

$\ heta_{t+1}=\ heta_{t}- \\dfrac{\\eta}{\\sqrt{\\hat{v}_t}+ \\epsilon}(\\beta_1 \\hat{m}_t + \\dfrac{(1 - \\beta_1) g_t}{1 - \\beta^t_1})$ ，

Adam中的 $\\hat{m}_{t-1}$ 换为 $\\hat{m}_t$

AMSGrad

ICLR2018提出的，文章指出Adam等优化器由于指数平均的方法使得对梯度的记忆是短期记忆，导致不能优化到全局最优点，泛化性能弱于SGD。AMSgrad中， $\\hat{v_t}$ 的更新方式改变为

$\\hat{v}_t=\ ext{max}(\\hat{v}_{t-1}, v_t)$

　无偏差修正估计的完整AMSGRAD更新如下：
$\\begin{align}\\begin{split}m_t &=\\beta_1 m_{t-1}+ (1 - \\beta_1) g_t \\\\ v_t &=\\beta_2 v_{t-1}+ (1 - \\beta_2) g_t^2\\\\ \\hat{v}_t &=\ ext{max}(\\hat{v}_{t-1}, v_t) \\\\ \ heta_{t+1}&=\ heta_{t}- \\dfrac{\\eta}{\\sqrt{\\hat{v}_t}+ \\epsilon}m_t \\end{split}\\end{align}$

Adabound

对学习率进行裁剪，对比AMSgrad效果更优

参考：

[1]An overview of gradient descent optimization algorithms

[2]https://openreview.net/pdf?id=Bkg3g2R9FX