参数优化方法(梯度下降、牛顿法、拟牛顿法、L-BFGS算法、共轭梯度法)

1. 分类

梯度法，共轭梯度法，牛顿法，拟牛顿法，蒙特卡洛法、Steepest Descent（SD）、L-BFGS等参数优化方法。

参数优化目标
在机器学习中，在定义好损失函数好，希望通过参数优化，使得损失函数最小。

2. 梯度下降法（最速下降法）

沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向（去负号），则就是更加容易找到函数的最小值。

在这里插入图片描述
里边的 $\lambda_k$ 是步长，常见是指定一个固定的比较小的常数，比如0.0001.

梯度下降法还可以分成：

批量梯度下降法（Batch Gradient Descent）
在更新参数时使用所有的样本来进行更新。
$\eta \cdot abla_ heta J( heta)$

这里的 $θ$ 可以看做是上述梯度下降法中的 $x$ .
随机梯度下降法（Stochastic Gradient Descent）
$\eta \cdot abla_ heta J( heta; x^{(i)}; y^{(i)})$
随机梯度下降法，与求梯度时没有用所有的样本的数据，而是仅仅选取一个样本来求梯度。

随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，但仅仅用一个样本决定梯度方向，导致解很有可能不是最优，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。
小批量梯度下降法（Mini-batch Gradient Descent）
$\eta \cdot abla_ heta J( heta; x^{(i:i+n)}; y^{(i:i+n)})$

小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，用一部分样本进行梯度计算。

缺点

靠近极小值时速度减慢。
直线搜索可能会产生一些问题。
可能会“之字型”地下降。

拓展：steepest descent
steepest descent,最陡下降。
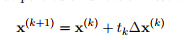
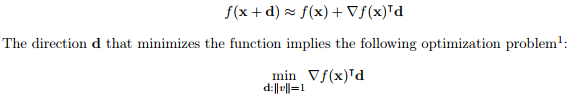
在这里插入图片描述

d 选取 2范数则为梯度下降：

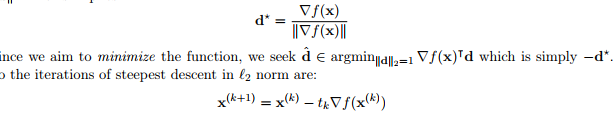
也可以选取 1 范数（ coordinate descent）：

3. 牛顿法

牛顿法的基本思想是利用目标函数的二次Taylor展开，并将其极小化。
在这里插入图片描述

牛顿法主要应用在两个方面，1：求方程的根；2：最优化。

(1) 求方程的根
牛顿法利用一阶泰勒展开：
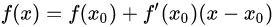
在这里插入图片描述
迭代方式：

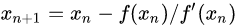
迭代后求得方程的根：

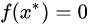
为什么这里迭代公式能够保证二次收敛到方程的根，可以看证明：Quadratic Convergence of Newton’s Method Michael Overton, Numerical Computing, Spring 2017 .

(2) 最优化（求取极值）
无约束最优化问题：
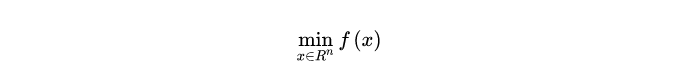
在这里插入图片描述
设 $x^{*}$ 为目标函数的极小点。

在这里插入图片描述

(3) 梯度下降和牛顿法的区别

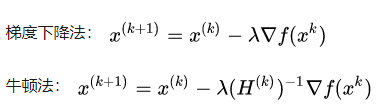
梯度下降法只使用了一阶信息（其实就是泰勒一阶展开，结合更新参数向量与梯度互为反方向时，更新最快，导出的公式）；
牛顿法使用了二阶海森矩阵的逆。
因此，牛顿法迭代次数更少就能收敛了。
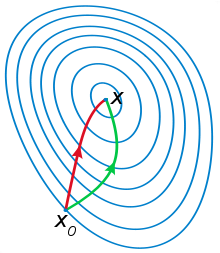
在这里插入图片描述
绿色为牛顿法，红色为梯度下降法。

4. 拟牛顿法

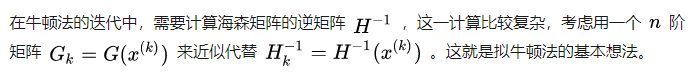
在这里插入图片描述
也就是在迭代中，正向进行迭代而不用求逆。

4.1 L-BFGS算法

一种非常流行和成功的拟牛顿法
Limited memory Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm

在这里插入图片描述
简单的思路是，之前的拟牛顿法需要保持矩阵，这里只需要使用向量 s, q 即可，节约内存开销。

5. 共轭梯度法

共轭梯度法，Conjugate gradient method，是一种求解对称正定线性方程组Ax=b的迭代方法。

共轭梯度法是介于梯度下降法与牛顿法之间的一个方法，是一个一阶方法。它克服了梯度下降法收敛慢的缺点，又避免了存储和计算牛顿法所需要的二阶导数信息。

适用
二次规划问题。
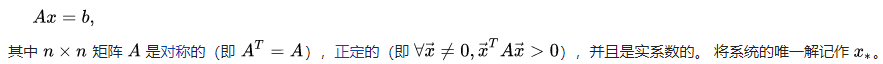
在这里插入图片描述
思想:
共轭梯度法的基本思想是把共轭性与最速下降法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。根据共轭方向的基本性质，这种方法具有二次终止性。

共轭梯度算法

算法用Gram-Schmidt找 n 个共轭向量。

在这里插入图片描述

6. 总结

在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

（1）牛顿法在什么时候只需要迭代一次就能求解，什么时候牛顿法不能适用？
对于正定二次函数，一步即可得最优解。

当初始点远离最优解时，Gk不一定是正定的，则牛顿方向不一定为下降方向，其收敛性不能保证。这说明恒取步长因子为1是不合适的，应该采用一维搜索（仅当步长因子 ${αk}$ 收敛1时，牛顿法才是二阶收敛的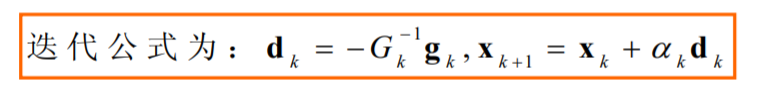）在这里插入图片描述
带步长因子的牛顿法是总体收敛的。
（2）拟牛顿法解决了牛顿法哪个问题？
Hesse矩阵的计算工作量大，有时目标函数的Hesse阵很难计算。
拟牛顿法利用目标函数和一阶导数，来构造目标函数的曲率近似，而不需要明显形成Hesse阵，同时
具有收敛速度快的优点。
在这里插入图片描述

最近开通了个公众号，主要分享推荐系统，风控等算法相关的内容，感兴趣的伙伴可以关注下。
在这里插入图片描述
公众号相关的学习资料会上传到QQ群596506387，欢迎关注。

参考：